Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cohen, J.W.
1973.
Asymptotic relations in queueing theory.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 2,
p.
107.
Pakes, A. G.
1975.
On the tails of waiting-time distributions.
Journal of Applied Probability,
Vol. 12,
Issue. 03,
p.
555.
Delbrouck, L.E.N.
1975.
Convexity properties, moment inequalities and asymptotic exponential approximations for delay distributions in G1/G/1 systems.
Stochastic Processes and their Applications,
Vol. 3,
Issue. 2,
p.
193.
Veraverbeke, N.
1977.
Asymptotic behaviour of Wiener-Hopf factors of a random walk.
Stochastic Processes and their Applications,
Vol. 5,
Issue. 1,
p.
27.
Alam, Khursheed
1978.
Asymptotic property of the distribution of the maxima of a random walk.
Stochastic Processes and their Applications,
Vol. 7,
Issue. 3,
p.
337.
Embrechts, Paul
Goldie, Charles M.
and
Veraverbeke, N.
1979.
Subexponential distribution functions and some applications.
Advances in Applied Probability,
Vol. 11,
Issue. 2,
p.
283.
Embrechts, Paul
Goldie, Charles M.
and
Veraverbeke, N.
1979.
Subexponential distribution functions and some applications.
Advances in Applied Probability,
Vol. 11,
Issue. 2,
p.
283.
Embrechts, Paul
Goldie, Charles M.
and
Veraverbeke, No�l
1979.
Subexponentiality and infinite divisibility.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 49,
Issue. 3,
p.
335.
Resnick, Sidney
and
Greenwood, Priscilla
1979.
A bivariate stable characterization and domains of attraction.
Journal of Multivariate Analysis,
Vol. 9,
Issue. 2,
p.
206.
Doney, R. A.
1980.
Moments of ladder heights in random walks.
Journal of Applied Probability,
Vol. 17,
Issue. 01,
p.
248.
De Meyer, A.
and
Teugels, J. L.
1980.
On the asymptotic behaviour of the distributions of the busy period and service time in M/G/1.
Journal of Applied Probability,
Vol. 17,
Issue. 3,
p.
802.
Asmussen, S�ren
1981.
Equilibrium properties of the M/G/1 queue.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 58,
Issue. 2,
p.
267.
Embrechts, Paul
and
Goldie, Charles M.
1982.
On convolution tails.
Stochastic Processes and their Applications,
Vol. 13,
Issue. 3,
p.
263.
Embrechts, Paul
and
Hawkes, John
1982.
A limit theorem for the tails of discrete infinitely divisible laws with applications to fluctuation theory.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 32,
Issue. 3,
p.
412.
1982.
The Single Server Queue.
Vol. 8,
Issue. ,
p.
676.
Gr�bel, Rudolf
1983.
�ber unbegrenzt teilbare Verteilungen.
Archiv der Mathematik,
Vol. 41,
Issue. 1,
p.
80.
Resnick, Sidney I.
1986.
Point processes, regular variation and weak convergence.
Advances in Applied Probability,
Vol. 18,
Issue. 1,
p.
66.
Omey, E.
and
Willekens, E.
1987.
Theory prob. appl..
Communications in Statistics. Stochastic Models,
Vol. 3,
Issue. 3,
p.
311.
Willekens, E.
and
Teugels, J. L.
1992.
Asymptotic expansions for waiting time probabilities in an M/G/1 queue with long-tailed service time.
Queueing Systems,
Vol. 10,
Issue. 4,
p.
295.
Abate, Joseph
Choudhury, Gagan L.
and
Whitt, Ward
1994.
Waiting-time tail probabilities in queues with long-tail service-time distributions.
Queueing Systems,
Vol. 16,
Issue. 3-4,
p.
311.
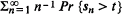 varies regularly at + ∞.
varies regularly at + ∞.

