Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T17:52:52.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Some results involving the maximum of Brownian motion

Part of: Stochastic processes

Published online by Cambridge University Press:  14 July 2016

R. A. Doney
R. A. Doney*
Affiliation:
University of Manchester
*
∗ Postal address: Statistical Laboratory, Department of Mathematics, The University, Manchester M13 9PL, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

If X is a Brownian motion with drift 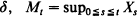and γ = inf{t > 0: Mt = t} we derive the joint density of the triple {U, γ, Δ}, where 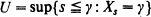and Δ= γ —Xγ. In the case δ = 0 it follows easily from this that Δ has an Exp(2) distribution and this in turn implies the rather surprising result that if τ= inf{t > 0: Xt = Mt = t}, then Pr{τ = 0} = 0 and 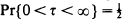. We also derive various other distributional results involving the pair (X, M), including for example the distribution of 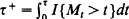; in particular we show that, in case δ. = 1, when Pr{0 < τ < ∞} = 1, the ratio τ+/τ has the arc-sine distribution.

Keywords

DENSITY FACTORIZATIONHITTING TIMESEXPONENTIAL BARRIERS

MSC classification

Primary: 60G17: Sample path properties
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 4 , December 1993 , pp. 805 - 818
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berman, S. M. (1982) Sojourns and extremes of a diffusion process on a fixed interval. Adv. Appl. Prob. 14, 811–832.Google Scholar
Doney, R. A. (1991) Hitting probabilities for spectrally positive Lévy processes. J. Lond. Math. Soc. (2) 44, 566–572.Google Scholar
Doney, R. A. (1993) A path decomposition for Lévy processes. Stoch. Proc. Appl. Google Scholar
Doney, R. A. and Grey, D. R. (1989) Some remarks on Brownian motion with drift. J. Appl. Prob. 26, 659–663.Google Scholar
Imhof, J.-P. (1984) Density factorizations for Brownian motion, meander and the three-dimensional Bessel process, and applications. J. Appl. Prob. 21, 500–510.Google Scholar
Imhof, J.-P. (1986) On the time spent above a level by Brownian motion with negative drift. Adv. Appl. Prob. 18, 1017–1018.Google Scholar
Rogers, C. J. (1984) A new identity for real Lévy processes. Ann. Inst. H. Poincaré 20, 21–34.Google Scholar
Williams, D. (1974) Path decomposition and continuity of local time for one-dimensional diffusions, I. Proc. Lond. Math. Soc. 28, 738–768.Google Scholar