Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T08:52:09.857Z Has data issue: false hasContentIssue false
  • English
  • Français

A simultaneous characterization of the Poisson and bernoulli distributions

Published online by Cambridge University Press:  14 July 2016

George Kimeldorf ,
Detlef Plachky  and
Allan R. Sampson
George Kimeldorf*
Affiliation:
University of Texas at Dallas
Detlef Plachky*
Affiliation:
Westfälische Wilhelms Universität
Allan R. Sampson*
Affiliation:
University of Pittsburgh
*
∗Postal address: Mathematical Sciences Program, University of Texas at Dallas, Richardson, TX 75080, U.S.A.
∗∗Postal address: Institute for Mathematical Statistics, Westfälische Wilhelms Universität, D-4400 Münster, W. Germany.
∗∗∗Postal address: Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, PA 15260, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

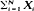Let N, X1, X2, · ·· be non-constant independent random variables with X1, X2, · ·· being identically distributed and N being non-negative and integer-valued. It is shown that the independence of and 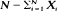implies that the Xi's have a Bernoulli distribution and N has a Poisson distribution. Other related characterization results are considered.

Keywords

CHARACTERIZATIONPOISSONBERNOULLIRAO–RUBIN CHARACTERIZATION
Type
Short Communications
Information
Journal of Applied Probability , Volume 18 , Issue 1 , March 1981 , pp. 316 - 320
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This author's work is sponsored in part by the Air Force Office of Scientific Research, Air Force Systems Command, under Contract No. F49620–79–C–0161.

References

Aczel, J. (1972) On a characterization of Poisson distributions. J. Appl. Prob. 9, 852–856.CrossRefGoogle Scholar
Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. Wiley, New York.Google Scholar
Haight, H. A. (1967) Handbook of the Poisson Distribution. Wiley, New York.Google Scholar
Kagan, A. M., Linnik, Yu. V. and Rao, C. R. (1973) Characterization Problems in Mathematical Statistics. Wiley, New York.Google Scholar
Moran, P. A. P. (1952) A characteristic property of the Poisson distribution. Proc. Camb. Phil. Soc. 48, 206–207.CrossRefGoogle Scholar
Patil, G. P. and Seshadri, V. (1964) Characterization theorems for some univariate probability distributions. J. R. Statist. Soc. B 26, 286–292.Google Scholar
Plachky, D. (1977) Note on sums of a random number of random variables with exponential family distribution. Comm. Statist. A 6, 1305–1309.CrossRefGoogle Scholar
Rao, C. R. and Rubin, H. (1964) On a characterization of the Poisson distribution. Sankhya A 26, 295–298.Google Scholar
Shanbhag, D. N. (1974) An elementary proof of the Rao–Rubin characterization of the Poisson distribution. J. Appl. Prob. 11, 211–215.CrossRefGoogle Scholar
Shanbhag, D. N. (1977) An extension of the Rao–Rubin characterization of the Poisson distribution. J. Appl. Prob. 14, 640–646.CrossRefGoogle Scholar
Talwalker, S. (1970) A characterization of the double Poisson distribution. Sankhya A 32, 265–270.Google Scholar