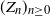Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
彭, 超
2024.
Cramer Moderate Deviations for a Supercritical Galton-Watson Process with Immigration.
Pure Mathematics,
Vol. 14,
Issue. 05,
p.
78.