Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-18T18:44:14.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-exciting multifractional processes

Part of: Stochastic analysis Stochastic processes

Published online by Cambridge University Press:  25 February 2021

Fabian A. Harang ,
Marc Lagunas-Merino  and
Salvador Ortiz-Latorre
Salvador Ortiz-Latorre*
Affiliation:
University of Oslo
*
*Postal address: Postboks 1053 Blindern, 0316 OSLO.
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a new multifractional stochastic process which allows for self-exciting behavior, similar to what can be seen for example in earthquakes and other self-organizing phenomena. The process can be seen as an extension of a multifractional Brownian motion, where the Hurst function is dependent on the past of the process. We define this by means of a stochastic Volterra equation, and we prove existence and uniqueness of this equation, as well as giving bounds on the p-order moments, for all 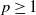$p\geq1$. We show convergence of an Euler–Maruyama scheme for the process, and also give the rate of convergence, which is dependent on the self-exciting dynamics of the process. Moreover, we discuss various applications of this process, and give examples of different functions to model self-exciting behavior.

Keywords

Multifractional stochastic processself-exciting processVolterra equationEuler–Maruyama schemeHurst exponent

MSC classification

Primary: 60G22: Fractional processes, including fractional Brownian motion
Secondary: 60H20: Stochastic integral equations 60H35: Computational methods for stochastic equations
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 22 - 41
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barndorff-Nielsen, O. E., Espen Benth, F. and Veraart, A. E. D. (2018). Ambit Stochastics (Probability Theory and Stochastic Modelling). Springer, Cham.CrossRefGoogle Scholar
Barrière, O., Echelard, A. and Véhel, L. (2012). Self-regulating processes. Electron. J. Prob. 17, 1–30.CrossRefGoogle Scholar
Benassi, A., Jaffard, S. and Roux, D. (1997). Elliptic Gaussian random processes. Rev. Mat. Iberoamericana 13, 19–90.CrossRefGoogle Scholar
Bianchi, S. and Pianese, A. (2015). Asset price modeling: from fractional to multifractional processes. In Future Perspectives in Risk Models and Finance (International Series in Operations Research & Management Science 211), pp. 247–285. Springer, Cham.CrossRefGoogle Scholar
Bianchi, S., Pantanella, A. and Pianese, A. (2013). Modeling stock prices by multifractional Brownian motion: an improved estimation of the pointwise regularity. Quant. Finance 13, 1317–1330.CrossRefGoogle Scholar
Cont, R. and Tankov, P. (2004). Financial Modelling with Jump Processes (Chapman & Hall/CRC Financial Mathematics Series). Chapman & Hall/CRC, Boca Raton.Google Scholar
Corlay, S., Lebovits, J. and Véhel, J. L. (2014). Multifractional stochastic volatility models. Math. Finance 24, 364–402.CrossRefGoogle Scholar
El Euch, O. and Rosenbaum, M. (2019). The characteristic function of rough Heston models. Math. Finance 29, 3–38.CrossRefGoogle Scholar
Gatheral, J., Jaisson, T. and Rosenbaum, M. (2018). Volatility is rough. Quant. Finance 18, 933–949.CrossRefGoogle Scholar
Hawkes, A. G. (2018). Hawkes processes and their applications to finance: a review. Quant. Finance 18, 193–198.CrossRefGoogle Scholar
Karatzas, I and Shreve, S. E. (1998). Brownian Motion and Stochastic Calculus, 2nd edn. Springer.CrossRefGoogle Scholar
Lebovits, J. and Véhel, J. L. (2014). White noise-based stochastic calculus with respect to multifractional Brownian motion. Stochastics 86, 87–124.CrossRefGoogle Scholar
Peltier, R.-F. and Véhel, J. L. (1995). Multifractional Brownian motion: definition and preliminary results. Research Report RR-2645, INRIA, Projet FRACTALES.Google Scholar
Pesquet-Popescu, B. and Véhel, J. L. (2002). Stochastic fractal models for image processing. IEEE Signal Process. Magazine 19, 48–62.CrossRefGoogle Scholar
Pianese, A., Bianchi, S. and Palazzo, A. M. (2018). Fast and unbiased estimator of the time-dependent Hurst exponent. Chaos 28, 031102.CrossRefGoogle ScholarPubMed
Riedi, R. and Véhel, J. L. (1997). Multifractal properties of TCP traffic: a numerical study. Research Report RR-3129, INRIA, Projet FRACTALES.Google Scholar
Sornette, D. and Filimonov, V. (2011). Self-excited multifractal dynamics. Europhys. Lett. Assoc. 94, 46003.Google Scholar
Ye, H., Gao, J. and Ding, Y. (2007). A generalized Gronwall inequality and its application to a fractional differential equation. J. Math. Anal. Appl. 328, 1075–1081.CrossRefGoogle Scholar
Zhang, X. (2008). Euler schemes and large deviations for stochastic Volterra equations with singular kernels. J. Differential Equat. 244, 2226–2250.CrossRefGoogle Scholar
Zhang, X. (2010). Stochastic Volterra equations in Banach spaces and stochastic partial differential equation. J. Funct. Anal. 258, 1361–1425.CrossRefGoogle Scholar