Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-29T05:18:39.102Z Has data issue: false hasContentIssue false
  • English
  • Français

Scheduled maxima sequences

Published online by Cambridge University Press:  14 July 2016

Joseph G. Deken
Joseph G. Deken*
Affiliation:
Princeton University
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a vector-valued scheduled maxima sequence M by considering simultaneously the maxima of several i.i.d. sequences, with the number of observations considered from each sequence at any time determined by a random scheduling sequence J. It is shown that the max-min (vector) sequence 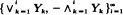derived from i.i.d. 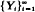can be represented as a mixture of scheduled maxima sequences, giving results for this sequence and the range 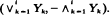A functional limit theorem for the scheduled maxima sequence shows convergence to independent extremal processes. Embedding in a scheduled extremal process gives strong laws, central limit theorems, and laws of the iterated logarithm for the record time of the scheduled maxima sequence, and hence for the max-min sequence and the range.

Keywords

MAXIMAMINIMARANGEWEAK CONVERGENCEFUNCTIONAL LIMIT THEOREMSEXTREMAL PROCESSESRECORD VALUESPOISSON PROCESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 15 , Issue 3 , September 1978 , pp. 543 - 551
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
De Haan, L. (1974) Weak limits of sample range. J. Appl. Prob. 11, 836–841.Google Scholar
Lamperti, J. (1964) On extreme order statistics. Ann. Math. Statist. 35, 1726–1737.Google Scholar
Lindvall, T. (1973) Weak convergence of probability measures and random functions in the space D(0, 8). J. Appl. Prob. 10, 109–121.CrossRefGoogle Scholar
Resnick, S. (1971) Tail equivalence and its applications. J. Appl. Prob. 8, 136–156.Google Scholar
Resnick, S. (1973) Extremal processes and record value times. J. Appl. Prob. 10, 864–868.CrossRefGoogle Scholar
Resnick, S. and Rubinovitch, M. (1973) The structure of extremal processes. Adv. Appl. Prob. 5, 287–307.CrossRefGoogle Scholar
Skorohod, A. V. (1956) Limit theorems for stochastic processes. Theory Prob. Appl. 1, 261–290.CrossRefGoogle Scholar
Whitt, W. (1973) Continuity of several functions on the function space D. Preprint, Department of Administrative Sciences, Yale University.Google Scholar