Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T02:47:56.943Z Has data issue: false hasContentIssue false
  • English
  • Français

Rate of strong convergence to Markov-modulated Brownian motion

Part of: Limit theorems Markov processes Stochastic processes

Published online by Cambridge University Press:  18 January 2022

Giang T. Nguyen Open the ORCID record for Giang T. Nguyen [Opens in a new window]  and
Oscar Peralta Open the ORCID record for Oscar Peralta [Opens in a new window]
Giang T. Nguyen*
Affiliation:
The University of Adelaide
Oscar Peralta*
Affiliation:
The University of Adelaide
*
*Postal address: The University of Adelaide, School of Mathematical Sciences, SA 5005, Australia.
*Postal address: The University of Adelaide, School of Mathematical Sciences, SA 5005, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Latouche and Nguyen (2015b) constructed a sequence of stochastic fluid processes and showed that it converges weakly to a Markov-modulated Brownian motion (MMBM). Here, we construct a different sequence of stochastic fluid processes and show that it converges strongly to an MMBM. To the best of our knowledge, this is the first result on strong convergence to a Markov-modulated Brownian motion. Besides implying weak convergence, such a strong approximation constitutes a powerful tool for developing deep results for sophisticated models. Additionally, we prove that the rate of this almost sure convergence is 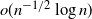$o(n^{-1/2} \log n)$ . 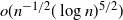When reduced to the special case of standard Brownian motion, our convergence rate is an improvement over that obtained by a different approximation in Gorostiza and Griego (1980), which is $o(n^{-1/2}(\log n)^{5/2})$ .

Keywords

Stochastic fluid modelMarkov-modulated Brownian motionstrong convergencefirst passage probability

MSC classification

Primary: 60G15: Gaussian processes
Secondary: 60F15: Strong theorems 60J27: Continuous-time Markov processes on discrete state spaces
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 1 , March 2022 , pp. 1 - 16
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, S. (2017). Time-dependent and stationary analyses of two-sided reflected Markov-modulated Brownian motion with bilateral PH-type jumps. J. Korean Statist. Soc., 46, 45–69.10.1016/j.jkss.2016.06.002CrossRefGoogle Scholar
Asmussen, S. (1995). Stationary distributions for fluid flow models with or without Brownian noise. Stoch. Models, 11, 21–49.CrossRefGoogle Scholar
Bean, N. G., O’Reilly, M. M. and Taylor, P. G. (2005). Algorithms for return probabilities for stochastic fluid flows. Stoch. Models, 21, 149–184.10.1081/STM-200046511CrossRefGoogle Scholar
Billingsley, P. (1999). Convergence of Probability Measures. John Wiley, Chichester.CrossRefGoogle Scholar
Bladt, M. and Nielsen, B. F. (2017). Matrix-Exponential Distributions in Applied Probability, Vol. 81. Springer, Berlin.Google Scholar
Goldstein, S. (1951). On diffusion by discontinuous movements, and on the telegraph equation. Quart. J. Mech. Appl. Math., 4, 129–156.CrossRefGoogle Scholar
Gorostiza, L. G. (1980). Rate of convergence of an approximate solution of stochastic differential equations. Stochastics, 3, 267–276.CrossRefGoogle Scholar
Gorostiza, L. G. and Griego, R. J. (1979). Strong approximation of diffusion processes by transport processes. J. Math. Kyoto Univ., 19, 91–103.Google Scholar
Gorostiza, L. G. and Griego, R. J. (1980). Rate of convergence of uniform transport processes to Brownian motion and application to stochastic integrals. Stochastics, 3, 291–303.CrossRefGoogle Scholar
Griego, R. J., Heath, D. and Ruiz-Moncayo, A. (1971). Almost sure convergence of uniform transport processes to Brownian motion. Ann. Math. Statist., 42, 1129–1131.10.1214/aoms/1177693346CrossRefGoogle Scholar
Kac, M. (1974). A stochastic model related to the telegrapher’s equation. Rocky Mount. J. Math., 4, 497–510.10.1216/RMJ-1974-4-3-497CrossRefGoogle Scholar
Latouche, G. and Nguyen, G. T. (2015a). Fluid approach to two-sided reflected Markov-modulated Brownian motion. Queueing Systems, 80, 105–125.10.1007/s11134-014-9432-8CrossRefGoogle Scholar
Latouche, G. and Nguyen, G. T. (2015b). The morphing of fluid queues into Markov-modulated Brownian motion. Stoch. Systems, 5, 62–86.10.1287/13-SSY133CrossRefGoogle Scholar
Latouche, G. and Nguyen, G. T. (2016). Feedback control: Two-sided Markov-modulated Brownian motion with instantaneous change of phase at boundaries. Performance Evaluation, 106, 30–49.CrossRefGoogle Scholar
Latouche, G. and Nguyen, G. T. (2017). Slowing time: Markov-modulated Brownian motions with a sticky boundary. Stoch. Models, 33, 297–321.10.1080/15326349.2017.1284000CrossRefGoogle Scholar
Latouche, G. and Simon, M. (2018). Markov-modulated Brownian motion with temporary change of regime at level zero. Methodology Comput. Appl. Prob., 20, 1199–1222.CrossRefGoogle Scholar
Pinsky, M. (1968). Differential equations with a small parameter and the central limit theorem for functions defined on a finite Markov chain. Prob. Theory Relat. Fields, 9, 101–111.Google Scholar
Ramaswami, V. (2013). A fluid introduction to Brownian motion and stochastic integration. In Matrix-Analytic Methods in Stochastic Models, eds. Latouche, G. et al., Springer, New York, pp. 209–225.CrossRefGoogle Scholar
Watanabe, T. (1968). Approximation of uniform transport process on a finite interval to Brownian motion. Nagoya Math. J., 32, 297–314.CrossRefGoogle Scholar
Willink, R. (2003). Relationships between central moments and cumulants, with formulae for the central moments of gamma distributions. Commun. Statist. Theory Meth., 32, 701–704.10.1081/STA-120018823CrossRefGoogle Scholar