Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Klüppelberg, Claudia
1988.
Subexponential distributions and integrated tails.
Journal of Applied Probability,
Vol. 25,
Issue. 1,
p.
132.
Embrechts, P.
and
Villasenor, J.A.
1988.
Ruin estimates for large claims.
Insurance: Mathematics and Economics,
Vol. 7,
Issue. 4,
p.
269.
Willekens, Eric
1988.
The structure of the class of subexponential distributions.
Probability Theory and Related Fields,
Vol. 77,
Issue. 4,
p.
567.
Klüppelberg, Claudia
1990.
Asymptotic ordering of distribution functions and convolution semigroups.
Semigroup Forum,
Vol. 40,
Issue. 1,
p.
77.
Cline, D.B.H.
and
Samorodnitsky, G.
1994.
Subexponentiality of the product of independent random variables.
Stochastic Processes and their Applications,
Vol. 49,
Issue. 1,
p.
75.
Embrechts, Paul
and
Schmidli, Hanspeter
1994.
Modelling of extremal events in insurance and finance.
ZOR Zeitschrift f�r Operations Research Mathematical Methods of Operations Research,
Vol. 39,
Issue. 1,
p.
1.
Baltrūnas, A.
1996.
A local limit theorem on one-sided large deviations for dominated-variation distributions.
Lithuanian Mathematical Journal,
Vol. 36,
Issue. 1,
p.
1.
Diaz, Francisco J.
1999.
Identifying Tail Behavior by Means of Residual Quantile Functions.
Journal of Computational and Graphical Statistics,
Vol. 8,
Issue. 3,
p.
493.
Liu, Zhen
Nain, Philippe
Towsley, Don
and
Zhang, Zhi-Li
1999.
Asymptotic behavior of a multiplexer fed by a long-range dependent process.
Journal of Applied Probability,
Vol. 36,
Issue. 1,
p.
105.
Liu, Zhen
Nain, Philippe
Towsley, Don
and
Zhang, Zhi-Li
1999.
Asymptotic behavior of a multiplexer fed by a long-range dependent process.
Journal of Applied Probability,
Vol. 36,
Issue. 01,
p.
105.
Omey, Edward
and
Teugels, Jef L.
2002.
Weighted renewal functions: a hierarchical approach.
Advances in Applied Probability,
Vol. 34,
Issue. 2,
p.
394.
Tang, Qihe
2003.
A NOTE ON THE SEVERITY OF RUIN IN THE RENEWAL MODEL WITH CLAIMS OF DOMINATED VARIATION.
Bulletin of the Korean Mathematical Society,
Vol. 40,
Issue. 4,
p.
663.
Baltrunas, A.
and
Omey, E.
2003.
Second-Order Renewal Theorem in the Finite-Means Case.
Theory of Probability & Its Applications,
Vol. 47,
Issue. 1,
p.
127.
Su, Chun
and
Tang, Qi-he
2003.
Characterizations on Heavy-tailed Distributions by Means of Hazard Rate.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 19,
Issue. 1,
p.
135.
Cai, Jun
and
Tang, Qihe
2004.
On max-sum equivalence and convolution closure of heavy-tailed distributions and their applications.
Journal of Applied Probability,
Vol. 41,
Issue. 1,
p.
117.
Ng, Kai W.
and
Tang, Qihe
2004.
Asymptotic behavior of tail and local probabilities for sums of subexponential random variables.
Journal of Applied Probability,
Vol. 41,
Issue. 1,
p.
108.
Li, Quan-Lin
and
Zhao, Yiqiang Q.
2005.
Heavy-tailed asymptotics of stationary probability vectors of Markov chains of gi/g/1 type.
Advances in Applied Probability,
Vol. 37,
Issue. 2,
p.
482.
Hu, Feng
Yin, Chuancun
and
Zong, Zhaojun
2005.
Tail equivalence relationships for ruin probabilities in several risk models.
Applied Stochastic Models in Business and Industry,
Vol. 21,
Issue. 6,
p.
499.
Tang, Qihe
2005.
The finite-time ruin probability of the compound Poisson model with constant interest force.
Journal of Applied Probability,
Vol. 42,
Issue. 03,
p.
608.
Su, Chun
Hu, Zhishui
Chen, Yu
and
Liang, Hanying
2007.
A wide class of heavy-tailed distributions and its applications.
Frontiers of Mathematics in China,
Vol. 2,
Issue. 2,
p.
257.


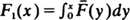 is subexponential. Here
is subexponential. Here 