Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T22:16:24.604Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of classes of life distribution based on the conditional variance

Part of: Survival analysis and censored data Operations research and management science

Published online by Cambridge University Press:  14 July 2016

Jordan Stoyanov  and
M. H. M. Al-Sadi
Jordan Stoyanov*
Affiliation:
University of Newcastle upon Tyne
M. H. M. Al-Sadi*
Affiliation:
University of Newcastle upon Tyne
*
∗ Postal address: School of Mathematics and Statistics, University of Newcastle upon Tyne, Newcastle upon Tyne, NE1 7RU, UK
∗ Postal address: School of Mathematics and Statistics, University of Newcastle upon Tyne, Newcastle upon Tyne, NE1 7RU, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider two classes of life distribution, V D and V I , the members of which are defined in terms of the conditional variance σ 2(t) of the remaining lifetime of a system: a life distribution F belongs to V D if 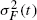is a decreasing function and to V I if 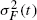is increasing. We study closure properties of these classes under relevant reliability operations such as mixing, convolution and formation of coherent systems. We show, for example, that the class V D is not closed under convolution or mixing, and that the class V I is not closed under formation of coherent systems.

Keywords

Conditional variancedecreasing-variance life distributionincreasing-variance life distributionmixingconvolutionformation of coherent system

MSC classification

Primary: 62N05: Reliability and life testing 90B25: Reliability, availability, maintenance, inspection
Type
Research Papers
Information
Journal of Applied Probability , Volume 41 , Issue 4 , December 2004 , pp. 953 - 960
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abouammoh, A. M., Kanjo, A., and Khalique, A. (1990). On some aspects of variance remaining life distributions. Microelectron. Reliability 30, 751–760.CrossRefGoogle Scholar
Barlow, R. E., and Proschan, F. (1981). Statistical Theory of Reliability and Life Testing. To Begin With, Silver Spring, MD.Google Scholar
Bhattacharjee, M. C., Abouammoh, A. M., Ahmed, A. N., and Barry, A. M. (2000). Preservation results for life distributions based on comparisons with asymptotic remaining life under replacement. J. Appl. Prob. 37, 999–1009.CrossRefGoogle Scholar
Bondesson, L. (1983). On preservation of classes of life distributions under reliability operations: some complementary results. Naval Res. Logist. Quart. 30, 443–447.CrossRefGoogle Scholar
Bryson, M. C., and Siddiqui, M. M. (1969). Some criteria for aging. J. Amer. Statist. Assoc. 64, 1472–1483.CrossRefGoogle Scholar
Dallas, A. C. (1981). A characterization using the conditional variance. Metrika 28, 151–153.CrossRefGoogle Scholar
Gupta, R. C., Kirmani, S. N. U. A., and Launer, R. L. (1987). On life distributions having monotone residual variance. Prob. Eng. Inf. Sci. 1, 299–307.CrossRefGoogle Scholar
Kopocińska, I. and Kopociński, B. (1985). The DMRL closure problem. Bull. Polish Acad. Sci. Ser. Math. 33, 425–429.Google Scholar
Launer, R. L. (1984). Inequalities for NBUE and NWUE life distributions. Operat. Res. 32, 660–667.CrossRefGoogle Scholar
Mitrinovic, D., Pecaric, J., and Fink, A. (1993). Classical and New Inequalities in Analysis. Kluwer, Dordrecht.CrossRefGoogle Scholar
Müller, A., and Stoyan, D. (2002). Comparison Methods for Stochastic Models and Risks. John Wiley, Chichester.Google Scholar