Probabilité de ruine éventuelle dans un modèle de risque à temps discret

Abstract

We continue the study of the discrete-time risk model introduced by Picard et al. (2003). The cumulative loss process (S_t)_t∊ℕ has independent and stationary increments, the increments per unit of time having nonnegative integer values with distribution {a_i, i ∊ ℕ and mean ā. The premium receipt process (c_k)_k∊ℕ is deterministic, nonnegative and nonuniform; in addition, we assume it to be regular in order for there to exist a constant c > ā such that the deviation 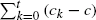is bounded as the time t varies. We are interested in whether or not ruin occurs within a finite time. If T is the time of ruin, we obtain P(T = ∞) as the limit of P(T > t) as t → ∞, firstly in the particular case where c = 1/d for some positive d ∊ ℕ, and then in the general case for positive c under the condition that a₀ > ½.

Résumé

On reprend le modèle de risque à temps discret introduit par Picard et al. (2003). Le processus des montants cumulés des sinistres (S_t)_t∊ℕ est un processus à accroissements indépendants et stationnaires dont les accroissements par unité de temps sont à valeurs naturelles de loi {a_i, i ∊ ℕ, avec moyenne ā. Le processus de rentrée des primes (c_k)_k∊ℕ est déterministe, non négatif et non uniforme, une hypothèse de régularité lui étant cependant imposée, à savoir l'existence d'une constante c > ā telle que, au cours du temps, l'écart 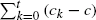reste borné. On s'intéresse à l'arrivée ou non de la ruine sur horizon infini. T étant la date de ruine, on obtient P(T = ∞) comme limite de P(T > t) pour t → ∞, d'abord dans le cas particulier où c = 1/d pour d ∊ ℕ positif, puis dans le cas général c positif quelconque moyennant ici la condition a₀ > ½.