Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T05:54:06.667Z Has data issue: false hasContentIssue false
  • English
  • Français

Prevalence of deficiency-zero reaction networks in an Erdös–Rényi framework

Part of: Graph theory Limit theorems

Published online by Cambridge University Press:  28 January 2022

David F. Anderson Open the ORCID record for David F. Anderson [Opens in a new window]  and
Tung D. Nguyen
David F. Anderson*
Affiliation:
University of Wisconsin-Madison
Tung D. Nguyen*
Affiliation:
University of Wisconsin-Madison, Texas A&M University
*
*Postal address: 617 Van Vleck Hall, 480 Lincoln Drive, Madison, WI 53706, USA. Email address: [email protected]
**Postal address: 601D Blocker Building, 155 Ireland St, College Station, TX 77840, USA. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Reaction networks are commonly used within the mathematical biology and mathematical chemistry communities to model the dynamics of interacting species. These models differ from the typical graphs found in random graph theory since their vertices are constructed from elementary building blocks, i.e. the species. We consider these networks in an Erdös–Rényi framework and, under suitable assumptions, derive a threshold function for the network to have a deficiency of zero, which is a property of great interest in the reaction network community. Specifically, if the number of species is denoted by n and the edge probability by 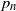$p_n$ , then we prove that the probability of a random binary network being deficiency zero converges to 1 if 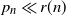$p_n\ll r(n)$ as 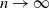$n \to \infty$ , and converges to 0 if 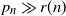$p_n \gg r(n)$ as 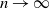$n \to \infty$ , where 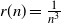$r(n)=\frac{1}{n^3}$ .

Keywords

DeficiencyErdös–Rényireaction networkrandom graphthreshold function

MSC classification

Primary: 60F99: None of the above, but in this section
Secondary: 05C80: Random graphs
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 384 - 398
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agazzi, A., Dembo, A. and Eckmann, J. P. (2018). Large deviations theory for Markov jump models of chemical reaction networks. Ann. Appl. Prob. 28, 1821–1855.10.1214/17-AAP1344CrossRefGoogle Scholar
Agazzi, A., Dembo, A. and Eckmann, J. P. (2018). On the geometry of chemical reaction networks: Lyapunov function and large deviations. J. Statist. Phys. 172, 321–352.10.1007/s10955-018-2035-8CrossRefGoogle Scholar
Anderson, D. F., Cappelletti, D., and Kurtz, T. G. (2017). Finite time distributions of stochastically modeled chemical systems with absolute concentration robustness. SIAM J. Appl. Dynam. Syst. 16, 1309–1339.10.1137/16M1070773CrossRefGoogle Scholar
Anderson, D. F. and Cotter, S. L. (2016). Product-form stationary distributions for deficiency zero networks with non-mass action kinetics. Bull. Math. Biol. 78, 2390–2407.10.1007/s11538-016-0220-yCrossRefGoogle ScholarPubMed
Anderson, D. F., Craciun, G., and Kurtz, T. G. (2010). Product-form stationary distributions for deficiency zero chemical reaction networks. Bull. Math. Biol. 72, 1947–1970.CrossRefGoogle ScholarPubMed
Anderson, D. F. and Nguyen, T. D. (2019). Results on stochastic reaction networks with non-mass action kinetics. Math. Biosci. Eng. 16, 2118–2140.CrossRefGoogle ScholarPubMed
Anderson, D. F. and Nguyen, T. D. (2021). Deficiency zero for random reaction networks under a stochastic block model framework. J. Math. Chem. 59, 2063–2097.CrossRefGoogle Scholar
Bollobás, B. and Thomason, A. (1987). Threshold functions. Combinatorica 7, 35–38.10.1007/BF02579198CrossRefGoogle Scholar
Cappelletti, D. and Wiuf, C. (2014). Product-form Poisson-like distributions and complex balanced reaction systems. SIAM J. Appl. Math. 76, 411–432.CrossRefGoogle Scholar
Chung, F. and Lu, L. (2002). The average distances in random graphs with given expected degrees. Proc. Nat. Acad. Sci. 99, 15879–15882.CrossRefGoogle Scholar
Feinberg, M. (1972). Complex balancing in general kinetic systems. Arch. Ration. Mech. Anal. 49, 187–194.10.1007/BF00255665CrossRefGoogle Scholar
Gopalkrishnan, M., Miller, E., and Shiu, A. (2014). A geometric approach to the global attractor conjecture. SIAM J. Appl. Dynam. Syst. 13, 758–797.CrossRefGoogle Scholar
Horn, F. (1972). Necessary and sufficient conditions for complex balancing in chemical kinetics. Arch. Ration. Mech. Anal. 49, 172–186.CrossRefGoogle Scholar
Horn, F. (1973). Stability and complex balancing in mass-action systems with three short complexes. Proc. R. Soc. London A 334, 331–342.CrossRefGoogle Scholar
Horn, F., and Jackson, R. (1972). General mass action kinetics. Arch. Ration. Mech. Anal. 47, 187–194.10.1007/BF00251225CrossRefGoogle Scholar
Peng, Z., Plum, A., Gagrani, P., and Baum, D. A. (2020). An ecological framework for the analysis of prebiotic chemical reaction networks. J. Theoret. Biol. 507, 110451.10.1016/j.jtbi.2020.110451CrossRefGoogle ScholarPubMed
Shinar, G. and Feinberg, M. (2010). Structural sources of robustness in biochemical reaction networks. Science 327, 1389–1391.10.1126/science.1183372CrossRefGoogle ScholarPubMed