Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T15:00:48.483Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial bounds for probability generating functions

Published online by Cambridge University Press:  14 July 2016

Henry Braun
Henry Braun*
Affiliation:
Princeton University
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem of approximating an arbitrary probability generating function (p.g.f.) 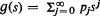by a polynomial 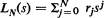is considered. It is shown that if the coefficients rj are chosen so that LN(·) agrees with g(·) to k derivatives at s = 1 and to (N – k) derivatives at s = 0, then LN is in fact an upper or lower bound to g; the nature of the bound depends only on k and not on N. Application of the results to the problems of finding bounds for extinction probabilities, extinction time distributions and moments of branching process distributions are examined.

Keywords

PROBABILITY GENERATING FUNCTIONSBRANCHING PROCESSESEXTINCTION TIME DISTRIBUTIONSMOMENT PROBLEM
Type
Research Papers
Information
Journal of Applied Probability , Volume 12 , Issue 3 , September 1975 , pp. 507 - 514
Copyright
Copyright © Applied Probability Trust 1975 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Agresti, A. (1973) Bounds on the extinction time distribution of a branching process. Technical Report , Department of Statistics, University of Florida (Gainesville).Google Scholar
[2] Brook, D. (1966) Bounds for moment generating functions and for extinction probabilities. J. Appl. Prob. 3, 171–178.Google Scholar
[3] Kingman, J. F. C. (1963) On inequalities of the Tchebyshev type. Proc. Camb. Phil. Soc. 59, 135–146.CrossRefGoogle Scholar