Article contents
A Poisson limit theorem for weakly exchangeable events
Published online by Cambridge University Press: 14 July 2016
Abstract
Let Y1, Y2, · ·· be a sequence of independent, identically distributed random variables, g some symmetric 0–1 function of m variables and set
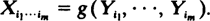 Silverman and Brown (1978) have shown that under certain conditions the statistic
Silverman and Brown (1978) have shown that under certain conditions the statistic
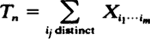 is asymptotically distributed as a Poisson random variable. They then use this result to derive limit distributions for various statistics, useful in the analysis of spatial data. In this paper, it is shown that Silverman and Brown's theorem holds under much weaker assumptions; assumptions which involve only the symmetry of the joint distributions of the Xil…im.
is asymptotically distributed as a Poisson random variable. They then use this result to derive limit distributions for various statistics, useful in the analysis of spatial data. In this paper, it is shown that Silverman and Brown's theorem holds under much weaker assumptions; assumptions which involve only the symmetry of the joint distributions of the Xil…im.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1979
References
- 4
- Cited by


