Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T08:02:37.872Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal stopping and maximal inequalities for geometric Brownian motion

Part of: Markov processes General theory in ordinary differential equations Stochastic processes

Published online by Cambridge University Press:  14 July 2016

S. E. Graversen  and
G. Peskir
S. E. Graversen*
Affiliation:
University of Aarhus
G. Peskir*
Affiliation:
University of Aarhus and University of Zagreb
*
∗Postal address: Institute of Mathematics, University of Aarhus, Ny Munkegade, 8000 Aarhus, Denmark
∗∗Postal address: 1. Institute of Mathematics, University of Aarhus, Ny Munkegade, 8000 Aarhus, Denmark. 2. Department of Mathematics, University of Zagreb, Bijenička 30, 10000 Zagreb, Croatia. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Explicit formulas are found for the payoff and the optimal stopping strategy of the optimal stopping problem supτE (max0≤t≤τXt − c τ), where X = (Xt)t≥0 is geometric Brownian motion with drift μ and volatility σ > 0, and the supremum is taken over all stopping times for X. The payoff is shown to be finite, if and only if μ < 0. 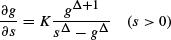The optimal stopping time is given by τ* = inf {t > 0 | Xt = g* (max0≤t≤sXs)} where s ↦ g*(s) is the maximal solution of the (nonlinear) differential equation under the condition 0 < g(s) < s, where Δ = 1 − 2μ / σ2 and K = Δ σ2 / 2c. The estimate is established g*(s) ∼ ((Δ − 1) / K Δ)1 / Δs1−1/Δ as s → ∞. Applying these results we prove the following maximal inequality: 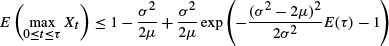where τ may be any stopping time for X. This extends the well-known identity E (supt>0Xt) = 1 − (σ 2 / 2 μ) and is shown to be sharp. The method of proof relies upon a smooth pasting guess (for the Stephan problem with moving boundary) and the Itô–Tanaka formula (being applied two-dimensionally). The key point and main novelty in our approach is the maximality principle for the moving boundary (the optimal stopping boundary is the maximal solution of the differential equation obtained by a smooth pasting guess). We think that this principle is by itself of theoretical and practical interest.

Keywords

Optimal stoppinggeometric Brownian motionStephan's problem with moving boundarythe principle of smooth fitmaximality principle for the optimal stopping boundaryPicard's method of successive approximationsItô–Tanaka formulaBurkholder–Gundy inequalityDoob's theoremcontinuous local martingale

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory 60J65: Brownian motion 34A34: Nonlinear equations and systems, general
Secondary: 60G44: Martingales with continuous parameter 60J60: Diffusion processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 35 , Issue 4 , December 1998 , pp. 856 - 872
Copyright
Copyright © Applied Probability Trust 1998 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Azema, J., and Yor, M. (1979). Une solution simple au problème de Skorokhod. In Sem. Prob. XIII (Lecture Notes in Mathematics 721), Springer, Berlin, pp. 90–115.Google Scholar
Black, F., and Scholes, M. (1973). The pricing of options and corporate liabilities. J. Pol. Econ. 81, 637–659.Google Scholar
Burkholder, D. L., and Gundy, R. F. (1970). Extrapolation and interpolation of quasi-linear operators on martingales. Acta Math. 124, 249–304.Google Scholar
Dubins, L. E., and Schwarz, G. (1965). On continuous martingales. Proc. Nat. Acad. Sci. USA 53, 913–916 Google Scholar
Dubins, L. E., Shepp, L. A., and Shiryaev, A. N. (1993). Optimal stopping rules and maximal inequalities for Bessel processes. Theory Prob. Appl. 38, 226–261.CrossRefGoogle Scholar
Graversen, S. E., and Peskir, G. (1998). On the Russian option: The expected waiting time. Theory Prob. Appl. 42, 416–425.CrossRefGoogle Scholar
Jacka, S. D. (1991). Optimal stopping and best constants for Doob-like inequalities I: The case p = 1. Ann. Prob. 19, 1798–1821.CrossRefGoogle Scholar
Peskir, G. (1998). Optimal stopping of the maximum process: The maximality principle. To appear in Ann. Prob.CrossRefGoogle Scholar
Revuz, D., and Yor, M. (1991). Continuous Martingales and Brownian Motion. Springer, Berlin.CrossRefGoogle Scholar
Shepp, L. A., and Shiryaev, A. N. (1993). The Russian option: reduced regret. Ann. Appl. Prob. 3, 631–640.Google Scholar