Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T11:16:37.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal redundancy allocation in coherent systems with heterogeneous dependent components

Part of: Operations research and management science Special processes Survival analysis and censored data

Published online by Cambridge University Press:  25 August 2022

Maryam Kelkinnama  and
Majid Asadi Open the ORCID record for Majid Asadi [Opens in a new window]
Maryam Kelkinnama*
Affiliation:
Isfahan University of Technology
Majid Asadi*
Affiliation:
University of Isfahan
*
*Postal address: Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran. Email address: [email protected]
**Postal address: Department of Statistics, University of Isfahan, Isfahan 81744, Iran, & School of Mathematics, Institute of Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the optimal number of redundant allocation to n-component coherent systems consisting of heterogeneous dependent components. We assume that the system is built up of L groups of different components, 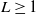$L\geq 1$ , where there are 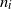$n_i$ components in group i, and 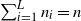$\sum_{i=1}^{L}n_i=n$ . The problem of interest is to allocate 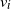$v_i$ active redundant components to each component of type i, 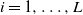$i=1,\dots, L$ . To get the optimal values of 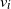$v_i$ we propose two cost-based criteria. One of them is introduced based on the costs of renewing the failed components and the costs of refreshing the alive ones at the system failure time. The other criterion is proposed based on the costs of replacing the system at its failure time or at a predetermined time $\tau$ , whichever occurs first. The expressions for the proposed functions are derived using the mixture representation of the system reliability function based on the notion of survival signature. We assume that a given copula function models the dependency structure between the components. In the particular case that the system is a series-parallel structure, we provide the formulas for the proposed cost-based functions. The results are discussed numerically for some specific coherent systems.

Keywords

Reliabilitycost optimalitysystem maintenancesurvival signatureactive redundancyexchangeability

MSC classification

Primary: 90B25: Reliability, availability, maintenance, inspection
Secondary: 60K10: Applications (reliability, demand theory, etc.) 62N05: Reliability and life testing
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 1144 - 1177
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashrafi, S. and Asadi, M. (2017). The failure probability of components in three-state networks with applications to age replacement policy. J. Appl. Prob. 54, 1051–1070.CrossRefGoogle Scholar
Bayramoglu Kavlak, K. (2017). Reliability and mean residual life functions of coherent systems in an active redundancy. Naval Res. Logist. 64, 19–28.CrossRefGoogle Scholar
Behboudi, Z., Borzadaran, G. M. and Asadi, M. (2021). Reliability modeling of two-unit cold standby systems: a periodic switching approach. Appl. Math. Model. 92, 176–195.CrossRefGoogle Scholar
Coolen, F. P. A. and Coolen-Maturi, T. (2013). Generalizing the signature to systems with multiple types of components. In Complex Systems and Dependability (Advances in Intelligent and Soft Computing 170), pp. 115–130. Springer, Berlin and Heidelberg.CrossRefGoogle Scholar
Dembinska, A. and Eryilmaz, S. (2021). Discrete time series-parallel system and its optimal configuration. Reliab. Eng. Syst. Saf. 215, 107832.CrossRefGoogle Scholar
Eryilmaz, S. (2017). The effectiveness of adding cold standby redundancy to a coherent system at system and component levels. Reliab. Eng. Syst. Saf. 165, 331–335.CrossRefGoogle Scholar
Eryilmaz, S. (2018). The number of failed components in a k-out-of-n system consisting of multiple types of components. Reliab. Eng. Syst. Saf. 175, 246–250.CrossRefGoogle Scholar
Eryilmaz, S. and Ucum, K. A. (2021). The lost capacity by the weighted k-out-of-n system upon system failure. Reliab. Eng. Syst. Saf. 216, 107914.CrossRefGoogle Scholar
Eryilmaz, S., Coolen, F. P. A. and Coolen-Maturi, T. (2018). Marginal and joint reliability importance based on survival signature. Reliab. Eng. Syst. Saf. 172, 118–128.CrossRefGoogle Scholar
Eryilmaz, S., Coolen, F. P. A. and Coolen-Maturi, T. (2018). Mean residual life of coherent systems consisting of multiple types of dependent components, applications to coherent systems. Naval Res. Logist. 65, 86–97.CrossRefGoogle Scholar
Eryilmaz, S., Özkurt, F. Y. and Rekan, T. E. (2020). The number of failed components in series-parallel system and its application to optimal design. Comput. Ind. Eng. 150, 106879.CrossRefGoogle Scholar
Fang, R. and Li, X. (2016). On allocating one active redundancy to coherent systems with dependent and heterogeneous components’ lifetimes. Naval Res. Logist. 63, 335–345.CrossRefGoogle Scholar
Fang, R. and Li, X. (2017). On matched active redundancy allocation for coherent systems with statistically dependent component lifetimes. Naval Res. Logist. 64, 580–598.CrossRefGoogle Scholar
Fang, R. and Li, X. (2018). On active redundancy allocation for coherent systems: from the viewpoint of minimal cut decomposition. Operat. Res. Lett. 46, 233–239.CrossRefGoogle Scholar
Fang, L., Balakrishnan, N. and Jin, Q. (2020). Optimal grouping of heterogeneous components in series-parallel and parallel-series systems under Archimedean copula dependence. J. Comput. Appl. Math. 377, 112916.CrossRefGoogle Scholar
Feng, G., Patelli, E., Beer, M. and Coolen, F. P. A. (2016). Imprecise system reliability and component importance based on survival signature. Reliab. Eng. Syst. Saf. 150, 116–125.CrossRefGoogle Scholar
Finkelstein, M., Hazra, N. K. and Cha, J. H. (2018). On optimal operational sequence of components in a warm standby system. J. Appl. Prob. 55, 1014–1024.CrossRefGoogle Scholar
Hashemi, M., Asadi, M. and Zarezadeh, S. (2020). Optimal maintenance policies for coherent systems with multi-type components. Reliab. Eng. Syst. Saf. 195, 106674.CrossRefGoogle Scholar
Huang, X., Coolen, F. P. A. and Coolen-Maturi, T. (2019). A heuristic survival signature based approach for reliability–redundancy allocation. Reliab. Eng. Syst. Saf. 185, 511–517.CrossRefGoogle Scholar
Karimi, B., Niaki, S. T. A., Miriha, S. M., Ghare Hasanluo, M. and Javanmard, S. (2019). A weighted K-means clustering approach to solve the redundancy allocation problem of systems having components with different failures. J. Risk. Reliab. 233, 925–942.Google Scholar
Li, X. and Ding, W. (2010). Optimal allocation of active redundancies to k-out-of-n systems with heterogeneous components. J. Appl. Prob. 47, 254–263.CrossRefGoogle Scholar
Mannai, N. and Gasmi, S. (2020). Optimal design of k-out-of-n system under first and last replacement in reliability theory. Operat. Res. 20, 1353–1368.CrossRefGoogle Scholar
Mizutani, S., Zhao, X. and Nakagawa, T. (2019). Random age replacement policies with periodic planning times. Internat. J. Reliab. Qual. Saf. Eng. 26, 1950023.CrossRefGoogle Scholar
Navarro, J. (2018). Distribution-free comparisons of residual lifetimes of coherent systems based on copula properties. Statist. Papers 59, 781–800.CrossRefGoogle Scholar
Navarro, J., Pellerey, F. and Di Crescenzo, A. (2015). Orderings of coherent systems with randomized dependent components. Europ. J. Operat. Res. 240, 127–139.CrossRefGoogle Scholar
Samaniego, F. J. (2007). System Signatures and their Applications in Engineering Reliability. Springer Science & Business Media.CrossRefGoogle Scholar
Samaniego, F. J. and Navarro, J. (2016). On comparing coherent systems with heterogenous components. Adv. Appl. Prob. 48, 88–111.CrossRefGoogle Scholar
Shen, J., Hu, J. and Ye, Z. S. (2020). Optimal switching policy for warm standby systems subjected to standby failure mode. IISE Trans. 52, 1262–1274.CrossRefGoogle Scholar
Soltani, R., Sadjadi, S. J. and Tavakkoli-Moghaddam, R. (2014). Robust cold standby redundancy allocation for nonrepairable series-parallel systems through Min-Max regret formulation and Benders’ decomposition method. J. Risk. Reliab. 228, 254–264.Google Scholar
Torrado, N. (2021). On allocation policies in systems with dependence structure and random selection of components. J. Comput. Appl. Math. 388, 113274.CrossRefGoogle Scholar
Torrado, N., Arriaza, A. and Navarro, J. (2021). A study on multi-level redundancy allocation in coherent systems formed by modules. Reliab. Eng. Syst. Saf. 213, 107694.CrossRefGoogle Scholar
You, Y., Fang, R. and Li, X. (2016). Allocating active redundancies to k-out-of-n reliability systems with permutation monotone component lifetimes. Appl. Stoch. Models Business Industry 32, 607–620.CrossRefGoogle Scholar
Zarezadeh, S. and Asadi, M. (2019). Coherent systems subject to multiple shocks with applications to preventative maintenance. Reliab. Eng. Syst. Saf. 185, 124–132.CrossRefGoogle Scholar
Zhang, Y. (2018). Optimal allocation of active redundancies in weighted k-out-of-n systems. Statist. Prob. Lett. 135, 110–117.CrossRefGoogle Scholar
Zhang, Y., Amini Seresht, E. and Ding, W. (2017). Component and system active redundancies for coherent systems with dependent components. Appl. Stoch. Models Business Industry 33, 409–421.Google Scholar
Zhao, X., Al-Khalifa, K. N., Hamouda, A. M. and Nakagawa, T. (2015). First and last triggering event approaches for replacement with minimal repairs. IEEE Trans. Reliab. 65, 197–207.CrossRefGoogle Scholar