Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T19:29:08.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal control of a finite dam: Wiener process input

Published online by Cambridge University Press:  14 July 2016

Lam Yeh  and
Lou Jiann Hua
Lam Yeh*
Affiliation:
The Chinese University of Hong Kong
Lou Jiann Hua*
Affiliation:
National University of Singapore
*
∗Postal address: Department of Statistics, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong.
∗∗Postal address: Department of Mathematics, National University of Singapore, Kent Ridge, Singapore 0511.
Get access Rights & Permissions [Opens in a new window]

Abstract

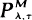The problem of optimal control of a finite dam in the class of policies has been considered by Lam Yeh [6], [7]. In this paper, by using the first Dynkin formula, the same problems of specifying an optimal policy in the class of the policies 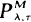to minimize the expected total discounted cost as well as the long-run average cost are considered. Both the expected total discounted cost and long-run average cost are determined explicitly, and then the optimal policy can be found numerically, Also, we obtain the transition density function and the resolvent operator of a reflecting Wiener process.

Keywords

WIENER PROCESSFIRST HITTING TIMESTRONG MARKOV PROPERTYCOST FUNCTIONALFIRST DYNKIN FORMULARESOLVENT OPERATOR
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 1 , March 1987 , pp. 186 - 199
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Attia, F. A. and Brockwell, P. J. (1982) The control of a finite dam. J. Appl. Prob. 19, 815–825.10.2307/3213834Google Scholar
[2]Faddy, M. J. (1974) Optimal control of finite dams: discrete (2-stage) output procedure. J. Appl. Prob. 11, 111–121.10.2307/3212588Google Scholar
[3]Freedman, D. (1971) Brownian Motion and Diffusion. Holden-Day, San Francisco.Google Scholar
[4]Karlin, S. and Taylor, H. M. (1975) A First Course in Stochastic Processes, 2nd edn. Academic Press, New York.Google Scholar
[5]Karlin, S. and Taylor, H. M. (1981) A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
[6]Yeh, Lam (1985) Optimal control of a finite dam: average-cost case. J. Appl. Prob. 22, 480–484.10.2307/3213793Google Scholar
[7]Yeh, Lam (1987) Optimal control of a finite dam — discounted cost case, Kexue Tongbao 32(2), 1–4.Google Scholar
[8]Zuckerman, D. (1977) Two-stage output procedure of a finite dam. J. Appl. Prob. 14, 421–425.Google Scholar