Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T15:04:04.214Z Has data issue: false hasContentIssue false
  • English
  • Français

On the single-server queue with non-homogeneous Poisson input and general service time

Published online by Cambridge University Press:  14 July 2016

A. M. Hasofer
A. M. Hasofer*
Affiliation:
University of Tasmania
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, a single-server queue with non-homogeneous Poisson input and general service time is considered. Particular attention is given to the case where the parameter of the Poisson input λ(t) is a periodic function of the time. The approach is an extension of the work of Takács and Reich . The main result of the investigation is that under certain conditions on the distribution of the service time, the form of the function λ(t) and the distribution of the waiting time at t = 0, the probability of a server being idle P0 and the Laplace transform Ω of the waiting time are both asymptotically periodic in t. 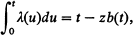Putting where b(t) is a periodic function of time, it is shown that both Po and Ω can be expanded in a power series in z, and a method for calculating explicitly the asymptotic values of the leading terms is obtained.

In many practical queueing problems, it is expected that the probability of arrivals will vary periodically. For example, in restaurants or at servicestations arrivals are more probable at rush hours than at slack periods, and rush hours are repeated day after day

Type
Research Papers
Information
Journal of Applied Probability , Volume 1 , Issue 2 , December 1964 , pp. 369 - 384
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bliss, C. I. (1958) Periodic regression in biology and climatology. Connecticut Agricultural Experiment Station, New Haven, Bull. 615.Google Scholar
[2] Doetsch, G. (1950) Handbuch der Laplace-Transformation. Verlag Birkhauser, Basel.Google Scholar
[3] Reich, E. (1958) and (1959) On the integro-differential equation of Takács I and II. Ann. Math. Statist. 29 and 30, 563–570 and 143-148.Google Scholar
[4] TakáCs, L. (1955) Investigation of waiting-time problems by reduction to Markov processes. Acta Math. Acad. Sci. Hungar. 6, 101–109.Google Scholar
[5] Tricomi, F. G. (1957) Integral Equations. Interscience Publishers, Inc., New York.Google Scholar