Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T06:24:18.107Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rate of convergence of Borovkov's multidimensional ergodic Markov chain

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

Akio Tanikawa
Akio Tanikawa*
Affiliation:
Kanazawa University
*
∗Postal address: Faculty of Engineering, Kanazawa University, 2-40-20 Kodatsuno, Kanazawa, Ishikawa 920, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with the multidimensional Markov chain {X(n)} = {X(x, n)}, considered by Borovkov [1], [2], [3], with the form X(n + 1) = ?(n) + ?(?(n), n), where the distribution of 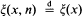depends only on x. Sufficient conditions on moments of |?(x)| are established for the Markov chain {X(n)} to have rate of convergence results (i.e. geometric ergodicity or sub-geometric rates for a variety of rate functions).

Keywords

MARKOV CHAINERGODICITYRATE OF CONVERGENCE

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Research Article
Information
Journal of Applied Probability , Volume 34 , Issue 2 , June 1997 , pp. 328 - 339
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Borovkov, A. A. (1990) Ergodicity and stability of multidimensional Markov chains. Theory Prob. Appl. 25, 542–546.Google Scholar
[2] Borovkov, A. A. (1990) Ergodicity and stability of Markov chains and their generalizations. Multidimensional chains. In Proc. 5th Int. Vilnius Conf. Vol. 1. Mokslas/VSP, Vilnius/Utrecht. pp. 179–188.Google Scholar
[3] Borovkov, A. A. (1991) Lyapunov functions and ergodicity of multi-dimensional Markov chains. Theory Prob. Appl. 36, 1–18.Google Scholar
[4] Dellacherie, C. and Meyer, P.-A. (1980) Probabilités et Potentiel. Herman, Paris.Google Scholar
[5] Fayolle, G., Malyshev, V. A., Menshikov, M. V. and Sidorenko, A. F. (1993) Lyapounov functions for Jackson networks. Math. Operat. Res. 18, 916–927.Google Scholar
[6] Foster, F. G. (1953) On the stochastic matrices associated with certain queueing processes. Ann. Math. Statist. 24, 355–360.Google Scholar
[7] Horduk, A. and Spieksma, F. M. (1992) On ergodicity and recurrence properties of a Markov chain with an application to an open Jackson network. Adv. Appl. Prob. 24, 343–376.Google Scholar
[8] Kingman, J. F. C. (1961) The ergodic behaviour of random walks. Biometrika 48, 391–396.Google Scholar
[9] Lamperti, J. (1960) Criteria for the recurrence or transience of stochastic process. I. J. Math. Anal. Appl. 1, 314–330.CrossRefGoogle Scholar
[10] Malyshev, V. A. (1972) Classification of two-dimensional positive random walks and almost linear semimartingales. Sov. Math. Dokl. 13, 136–139.Google Scholar
[11] Malyshev, V. A. and Menshikov, M. V. (1979) Ergodicity, continuity and analyticity of countable Markov chains. Trans. Moscow Math. Soc. 39, 2–48.Google Scholar
[12] Meyn, S. P. and Tweedie, R. L. (1993) Markov Chains and Stochastic Stability. Springer, Berlin.Google Scholar
[13] Nummelin, E. and Tuominen, P. (1982) Geometric ergodicity of Harris recurrent Markov chains with application to renewal theory. Stoch. Proc. Appl. 12, 187–202.Google Scholar
[14] Nummelin, E. and Tuominen, P. (1983) The rate of convergence in Orey's theorem for Harris recurrent Markov chains with applications to renewal theory. Stoch. Proc. Appl. 15, 295–311.Google Scholar
[15] Spieksma, F. M. (1991) Geometric ergodicity of the ALOHA-system and a coupled processors model. Prob. Eng. Inf. Sci. 5, 15–42.Google Scholar
[16] Spieksma, F. M. (1992) A recurrence type characterisation of µ-exponential ergodicity for Markov processes. Technical Report. University of Leiden.Google Scholar
[17] Spieksma, F. M. and Tweedie, R. L. (1994) Strengthening ergodicity to geometric ergodicity for Markov chains. Commun. Statist. Stoch. Models. 10, 45–74.CrossRefGoogle Scholar
[18] Tanikawa, A. (1996) The rate of convergence of a homogeneous Markov chain arising from two-queue networks. Comput. Math. Appl. 31, 103–109.Google Scholar
[19] Thorisson, H. (1985) The queue GI/G/1: Finite moments of the cycle variables and uniform rates of convergence. Stoch. Proc. Appl. 19, 83–99.Google Scholar
[20] Tweedie, R. L. (1976) Criteria for classifying general Markov chains. Adv. Appl. Prob. 8, 737–771.Google Scholar
[21] Tweedie, R. L. (1983) Criteria for rates of convergence of Markov chains, with application to queueing and storage theory. In Probability, Statistics and Analysis. ed. Kingman, J. F. C. and Reuter, G. E. H. Cambridge University Press, Cambridge. pp. 260–276.Google Scholar