Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kudlaev, E. M.
1990.
Divisible statistics.
Journal of Soviet Mathematics,
Vol. 50,
Issue. 3,
p.
1601.
Calka, Pierre
2002.
The distributions of the smallest disks containing the Poisson-Voronoi typical cell and the Crofton cell in the plane.
Advances in Applied Probability,
Vol. 34,
Issue. 4,
p.
702.
Calka, Pierre
2002.
La loi du plus petit disque contenant la cellule typique de Poisson–Voronoi.
Comptes Rendus. Mathématique,
Vol. 334,
Issue. 4,
p.
325.
Porret-Blanc, Sylvain
2007.
Sur le caractère borné de la cellule de Crofton des mosaïques de géodésiques dans le plan hyperbolique.
Comptes Rendus. Mathématique,
Vol. 344,
Issue. 8,
p.
477.
Arnold, Barry C.
2007.
Majorization: Here, There and Everywhere.
Statistical Science,
Vol. 22,
Issue. 3,
Leeuwaarden, J. S. H. van
Löpker, A. H.
and
Janssen, A. J. E. M.
2010.
Connecting Renewal Age Processes with M/D/1 and M/D/∞ Queues Through Stick Breaking.
Stochastic Models,
Vol. 26,
Issue. 1,
p.
141.
Chu, Yu-Ming
Xia, Wei-Feng
and
Zhang, Xiao-Hui
2012.
The Schur concavity, Schur multiplicative and harmonic convexities of the second dual form of the Hamy symmetric function with applications.
Journal of Multivariate Analysis,
Vol. 105,
Issue. 1,
p.
412.
2018.
Methods for Reliability Improvement and Risk Reduction.
p.
251.
Arnold, Barry C.
and
Sarabia, José María
2018.
Majorization and the Lorenz Order with Applications in Applied Mathematics and Economics.
p.
211.
2023.
Majorization and its Applications on Some Functions.
Australian Journal of Engineering and Innovative Technology,
p.
1.
Krapivsky, P L
2023.
Random sequential covering.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2023,
Issue. 3,
p.
033202.
Viot, Pascal
and
Krapivsky, P L
2025.
Random sequential covering of a one-dimensional lattice by k-mers.
Journal of Statistical Mechanics: Theory and Experiment,
Vol. 2025,
Issue. 1,
p.
013202.


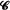 having unit length. Let
having unit length. Let 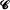 is completely covered by the
is completely covered by the 