Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-12T19:47:25.632Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of runs for Bernoulli arrays

Part of: Distribution theory - Probability Special processes Combinatorial probability

Published online by Cambridge University Press:  14 July 2016

Djilali Ait Aoudia  and
Éric Marchand
Djilali Ait Aoudia*
Affiliation:
Université de Sherbrooke
Éric Marchand*
Affiliation:
Université de Sherbrooke
*
∗Current address: Département de Mathématiques et de Statistique, Université de Montréal, Montréal, QC H3C 3J7, Canada.
∗∗Postal address: Département de Mathématiques, Université de Sherbrooke, Sherbrooke, QC J1K 2R1, Canada. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce and motivate the study of (n + 1) × r arrays X with Bernoulli entries Xk,j and independently distributed rows. We study the distribution of 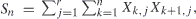which denotes the number of consecutive pairs of successes (or runs of length 2) when reading the array down the columns and across the rows. With the case r = 1 having been studied by several authors, and permitting some initial inferences for the general case r > 1, we examine various distributional properties and representations of Sn for the case r = 2, and, using a more explicit analysis, the case of multinomial and identically distributed rows. Applications are also given in cases where the array X arises from a Pólya sampling scheme.

Keywords

BernoullimultinomialPólya urnprobability generating functionruns

MSC classification

Secondary: 60C05: Combinatorial probability 60E05: Distributions 60K99: None of the above, but in this section
Type
Research Article
Information
Journal of Applied Probability , Volume 47 , Issue 2 , June 2010 , pp. 367 - 377
Copyright
Copyright © Applied Probability Trust 2010 

References

[1] Ait Aoudia, D. and Marchand, É. (2009). On the number of runs of Bernoulli arrays. Res. Rep. 76, Université de Sherbrooke. Available at: http://www.usherbrooke.ca/mathematiques/recherche/publications/rapports-recherche/.Google Scholar
[2] Ardakov, K. (1997). Powers and other functions of 2×2 matrices. Math. Gazette 4, 434–431.Google Scholar
[3] Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. II. John Wiley, New York.Google Scholar
[4] Holst, L. (2007). Counts of failure strings in certain Bernouilli sequences. J. Appl. Prob. 44, 824–830.Google Scholar
[5] Holst, L. (2008). The number of two-consecutive successes in a Hoppe–Polyá urn. J. Appl. Prob. 45, 901–906.Google Scholar
[6] Huffer, W. F., Sethuraman, J. and Sethuraman, S. (2009). A study of counts of Bernoulli strings via conditional Poisson processes. Proc. Amer. Math. Soc. 137, 2125–2134.Google Scholar
[7] Joffe, A., Marchand, É., Perron, F. and Popadiuk, P. (2004). On sums of products of Bernoulli variables and random permutations. J. Theoret. Prob. 17, 285–292.Google Scholar
[8] Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Applications. John Wiley, New York.Google Scholar
[9] Móri, T. F. (2001). On the distribution of sums of overlapping products. Acta Sci. Math. 67, 833–841.Google Scholar
[10] Sethuraman, J. and Sethuraman, S. (2004). On counts of Bernoulli strings and connections to rank orders and random permutations. A Festschrift for Herman Rubin (IMS Lecture Notes Monogr. Ser. 45), Institute of Mathematical Statistics, Beachwood, OH, pp. 140–152.CrossRefGoogle Scholar
[11] Stein, C. (1972). A bound for the error in the normal approximation to the distribution of a sum of dependent random variables. In Proc. 6th Berkeley Symp. Math. Statist. Prob., Vol. II, University of California Press, Berkeley, pp. 583–602.Google Scholar