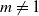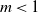1. Introduction and main result
Stochastic branching systems are famous mathematical models that describe the population size growth of reproductive individuals. The Bienaymé–Galton–Watson (BGW) model, originally developed as a family survival model in the second half of the 19th century, is a simple branching system. Due to the integration of various scientific areas, there are currently numerous generalizations and modifications of the BGW model. This motivated the search for new applications of branching models, which had a significant impact on the development of the theory of population dynamics. The most common models of branching schemes and related interpretations can be found in [Reference Asmussen and Hering1, Reference Athreya and Ney2, Reference Haccou, Jagers and Vatutin5, Reference Harris6, Reference Jagers11, Reference Kimmel and Axelrod12, Reference Sevastyanov17]. Many different specialized branching models related to other areas of stochastic analysis are available. Recent results on such modified models can be found, for example, in [Reference Gonzàlez4], which studies the asymptotic properties of continuous-time controlled branching systems and their modifications in the form of regenerative controlled branching systems, and in [Reference Li, Cheng and Li14], where explicit estimates of convergence rates are obtained in ratio limit type theorems for continuous-time Markovian branching-immigration systems. We consider the ordinary BGW system, which describes the evolution of the population size in a system of monotypic individuals capable of death and transformation into a random number of the same type of individuals. Although the BGW system has been studied quite deeply, it seems useful to discuss and improve some well-known classical facts from this theory in more detail. This paper is devoted to the well-known theorem related to the name of A. Kolmogorov [Reference Kolmogorov13].
Let Z(n) be a population size at the moment
![]() $n\in\mathbb{N}_0$
in the BGW system with branching rates
$n\in\mathbb{N}_0$
in the BGW system with branching rates
![]() $\{{p_k, k\in\mathbb{N}_0}\}$
, where
$\{{p_k, k\in\mathbb{N}_0}\}$
, where
![]() $\mathbb{N}_0=\{0\}\cup\mathbb{N}$
and
$\mathbb{N}_0=\{0\}\cup\mathbb{N}$
and
![]() $\mathbb{N}=\{1,2, \ldots\}$
. Namely, each individual in the system lives a unit-length lifetime and then gives
$\mathbb{N}=\{1,2, \ldots\}$
. Namely, each individual in the system lives a unit-length lifetime and then gives
![]() $k\in\mathbb{N}_0$
descendants with probability
$k\in\mathbb{N}_0$
descendants with probability
![]() $p_k$
. This is a reducible, homogeneous discrete-time Markov chain with a state space consisting of two classes:
$p_k$
. This is a reducible, homogeneous discrete-time Markov chain with a state space consisting of two classes:
![]() $\mathcal{S}_0=\{0\}\cup\mathcal{S}$
, where
$\mathcal{S}_0=\{0\}\cup\mathcal{S}$
, where
![]() $\{0\}$
is an absorbing state, and
$\{0\}$
is an absorbing state, and
![]() $\mathcal{S}\subset\mathbb{N}$
, which is the class of possible essential communicating states. Its transition probabilities are
$\mathcal{S}\subset\mathbb{N}$
, which is the class of possible essential communicating states. Its transition probabilities are
for any
![]() $i,j\in\mathcal{S}_0$
, where
$i,j\in\mathcal{S}_0$
, where
![]() $p_k=P_{1k}$
and
$p_k=P_{1k}$
and
![]() $\sum_{k\in\mathcal{S}_0}{p_k}=1$
. This is the branching property, which means that our BGW system is completely determined by the offspring law
$\sum_{k\in\mathcal{S}_0}{p_k}=1$
. This is the branching property, which means that our BGW system is completely determined by the offspring law
![]() $\{{p_k, k\in\mathcal{S}_0}\}$
. Conversely, any chain that satisfies the property (1.1) is a BGW system with the offspring law
$\{{p_k, k\in\mathcal{S}_0}\}$
. Conversely, any chain that satisfies the property (1.1) is a BGW system with the offspring law
![]() $\{{p_k}\}$
; see [Reference Athreya and Ney2, pp. 1–2] and [Reference Jagers11, p. 19]. To avoid trivial cases, it is assumed everywhere that
$\{{p_k}\}$
; see [Reference Athreya and Ney2, pp. 1–2] and [Reference Jagers11, p. 19]. To avoid trivial cases, it is assumed everywhere that
![]() $p_0+p_1<1$
and
$p_0+p_1<1$
and
![]() $m\;:\!=\;\sum_{k\in\mathcal{S}}{kp_k}<\infty$
. We consider the case of the Schröder BGW system, i.e.
$m\;:\!=\;\sum_{k\in\mathcal{S}}{kp_k}<\infty$
. We consider the case of the Schröder BGW system, i.e.
![]() $p_0+p_1>0$
.
$p_0+p_1>0$
.
Consider the n-step transition probabilities
![]() $P_{ij}(n) \;:\!=\; \mathbb{P}_i\{Z(n)=j\}$
, where
$P_{ij}(n) \;:\!=\; \mathbb{P}_i\{Z(n)=j\}$
, where
![]() $\mathbb{P}_i\{\ast\} \;:\!=\; \mathbb{P}\{\ast \mid {Z(0)=i}\}$
. Using the branching property (1.1) and the Kolmogorov–Chapman equation, we observe that
$\mathbb{P}_i\{\ast\} \;:\!=\; \mathbb{P}\{\ast \mid {Z(0)=i}\}$
. Using the branching property (1.1) and the Kolmogorov–Chapman equation, we observe that
for
![]() $s \in[0,1)$
, where the probability-generating function (GF)
$s \in[0,1)$
, where the probability-generating function (GF)
![]() $f_n(s)=\mathbb{E}_1 s^{Z(n)}$
is an n-fold iteration of the GF
$f_n(s)=\mathbb{E}_1 s^{Z(n)}$
is an n-fold iteration of the GF
![]() $f(s)\;:\!=\;\sum_{k\in\mathcal{S}_0}{p_k s^k}$
, i.e.
$f(s)\;:\!=\;\sum_{k\in\mathcal{S}_0}{p_k s^k}$
, i.e.
![]() $f_{n+1}(s)=f(f_n(s))=f_n(f(s))$
. So the offspring law
$f_{n+1}(s)=f(f_n(s))=f_n(f(s))$
. So the offspring law
![]() $\{{p_k, k\in\mathcal{S}_0}\}$
fully defines the structure of the BGW system. Furthermore, we can consider the asymptotic behaviours of the system states due to the iteration of the GF f(s). Defining q to be the smallest root of the fixed-point equation
$\{{p_k, k\in\mathcal{S}_0}\}$
fully defines the structure of the BGW system. Furthermore, we can consider the asymptotic behaviours of the system states due to the iteration of the GF f(s). Defining q to be the smallest root of the fixed-point equation
![]() $f(s)=s$
for
$f(s)=s$
for
![]() $s\in[0,1]$
, we recall that
$s\in[0,1]$
, we recall that
![]() $\lim_{n\to\infty}f_n(s)=q$
uniformly in
$\lim_{n\to\infty}f_n(s)=q$
uniformly in
![]() $s\in[0,r]$
for any fixed
$s\in[0,r]$
for any fixed
![]() $r<1$
. This root is an extinction probability of the system initiated by a single founder; see [Reference Athreya and Ney2, Chapter I]. Thus, the BGW system is a discrete dynamic system generated by the GF f(s) and with the fixed point q.
$r<1$
. This root is an extinction probability of the system initiated by a single founder; see [Reference Athreya and Ney2, Chapter I]. Thus, the BGW system is a discrete dynamic system generated by the GF f(s) and with the fixed point q.
Wherever necessary, we will write
![]() $\mathbb{E}$
and
$\mathbb{E}$
and
![]() $\mathbb{P}$
instead of
$\mathbb{P}$
instead of
![]() $\mathbb{E}_1$
and
$\mathbb{E}_1$
and
![]() $\mathbb{P}_1$
respectively.
$\mathbb{P}_1$
respectively.
Suppose now that the series
![]() $m\;:\!=\;\sum_{k\in\mathcal{S}}{kp_k}$
converges. Then
$m\;:\!=\;\sum_{k\in\mathcal{S}}{kp_k}$
converges. Then
![]() $m=f'(1-)$
and this is the offspring mean of the direct descendants of one individual over one generation of the time step. Using (1.2), in particular we can find that
$m=f'(1-)$
and this is the offspring mean of the direct descendants of one individual over one generation of the time step. Using (1.2), in particular we can find that
![]() $\mathbb{E}{Z(n)}=m^{n}$
. Using this, three classes of the BGW system are distinguished depending on the value of the parameter m. The system
$\mathbb{E}{Z(n)}=m^{n}$
. Using this, three classes of the BGW system are distinguished depending on the value of the parameter m. The system
![]() $\{Z(n)\}$
is called subcritical if
$\{Z(n)\}$
is called subcritical if
![]() $m<1$
, critical if
$m<1$
, critical if
![]() $m=1$
, and supercritical if
$m=1$
, and supercritical if
![]() $m>1$
. The extinction probability of subcritical and critical systems is equal to 1, while in the supercritical case
$m>1$
. The extinction probability of subcritical and critical systems is equal to 1, while in the supercritical case
![]() $q<1$
. Moreover, the sequence of vanishing probabilities
$q<1$
. Moreover, the sequence of vanishing probabilities
![]() $\{P_{10}(n)\}$
of direct descendants of the single founder-individual at time n tends monotonically to q as
$\{P_{10}(n)\}$
of direct descendants of the single founder-individual at time n tends monotonically to q as
![]() $n\to\infty$
; see [Reference Athreya and Ney2, Chapter I].
$n\to\infty$
; see [Reference Athreya and Ney2, Chapter I].
In what follows, we consider the noncritical case. Let
![]() $R_n(s)\;:\!=\;q-f_n(s)$
.
$R_n(s)\;:\!=\;q-f_n(s)$
.
In 1938 [Reference Kolmogorov13] established that the survival probability of the subcritical system
![]() $Q(n)\;:\!=\;\mathbb{P}\{{Z(n)>0}\}=R_n(0)$
admits the asymptotic representation
$Q(n)\;:\!=\;\mathbb{P}\{{Z(n)>0}\}=R_n(0)$
admits the asymptotic representation
if and only if
![]() $f''(1-)<\infty$
, where
$f''(1-)<\infty$
, where
![]() $\mathcal{K}$
is a positive constant depending on the numerical parameters of the offspring law
$\mathcal{K}$
is a positive constant depending on the numerical parameters of the offspring law
![]() $\{{p_k, k\in\mathcal{S}_0}\}$
, called the Kolmogorov constant, but the author did not calculate it in an explicit form. The same problem remains open for the continuous-time case. In this regard, [Reference Zolotarev18] regretted the absence of an explicit expression for this constant. Kolmogorov’s result (1.3) implies that on positive trajectories of the subcritical system
$\{{p_k, k\in\mathcal{S}_0}\}$
, called the Kolmogorov constant, but the author did not calculate it in an explicit form. The same problem remains open for the continuous-time case. In this regard, [Reference Zolotarev18] regretted the absence of an explicit expression for this constant. Kolmogorov’s result (1.3) implies that on positive trajectories of the subcritical system
![]() $\{Z(n)\}$
, the expectation of the individuals’ population stabilizes and approaches
$\{Z(n)\}$
, the expectation of the individuals’ population stabilizes and approaches
![]() ${1}/\mathcal{K}$
. Indeed, it follows that
${1}/\mathcal{K}$
. Indeed, it follows that
In addition to the above, due to the last relation, the constant
![]() $\mathcal{K}$
can be interpreted as an equivalence ratio of the expectation
$\mathcal{K}$
can be interpreted as an equivalence ratio of the expectation
![]() $\mathbb{E}{Z(n)}=m^{n}$
of the population size to the survival probability
$\mathbb{E}{Z(n)}=m^{n}$
of the population size to the survival probability
![]() ${\mathbb{P}\{{Z(n)>0}\}}$
of the system. Thus, it is of principal interest to obtain an explicit expression for this coefficient depending on the numerical parameters of the system under consideration.
${\mathbb{P}\{{Z(n)>0}\}}$
of the system. Thus, it is of principal interest to obtain an explicit expression for this coefficient depending on the numerical parameters of the system under consideration.
Later, in 1967, [Reference Nagaev and Badalbaev15] proved that
![]() $\mathbb{E}{Z(n)}$
and Q(n) vary (decrease) asymptotically equivalently even under the weaker condition
$\mathbb{E}{Z(n)}$
and Q(n) vary (decrease) asymptotically equivalently even under the weaker condition
In this situation, the equivalence ratio
![]() $\mathcal{K}$
in (1.3) certainly cannot depend on the second moment
$\mathcal{K}$
in (1.3) certainly cannot depend on the second moment
![]() $f''(1-)$
; it depends only on the sum of the convergent series in
$f''(1-)$
; it depends only on the sum of the convergent series in
![]() $\sum_{k\in{\mathcal{S}}}{p_{k}k\ln{k}}$
, but it still remains not calculated explicitly.
$\sum_{k\in{\mathcal{S}}}{p_{k}k\ln{k}}$
, but it still remains not calculated explicitly.
Another result on this issue [Reference Seneta16, Theorem 2(1)] states that if the condition (1.4) is satisfied, then
where
![]() $\mu\;:\!=\;\sum_{k\in{\mathcal{S}}}{k\mu_{k}}$
and
$\mu\;:\!=\;\sum_{k\in{\mathcal{S}}}{k\mu_{k}}$
and
![]() $\mu_{k}=\lim_{n\to\infty}\mathbb{P}\{{Z(n)=k\mid {Z(n)>0}}\}$
is the limiting invariant distribution for subcritical BGW systems. Seneta’s result certainly implies that
$\mu_{k}=\lim_{n\to\infty}\mathbb{P}\{{Z(n)=k\mid {Z(n)>0}}\}$
is the limiting invariant distribution for subcritical BGW systems. Seneta’s result certainly implies that
![]() $\mathcal{K}={1}/{\mu}$
, but the problem is that the explicit form of the limit parameter
$\mathcal{K}={1}/{\mu}$
, but the problem is that the explicit form of the limit parameter
![]() ${\mu}$
, depending on the structural parameters of the BGW system such as the offspring mean m and variance, has not been found.
${\mu}$
, depending on the structural parameters of the BGW system such as the offspring mean m and variance, has not been found.
This circumstance makes it difficult to complete the assertions of a number of limit theorems in the theory of subcritical BGW systems.
We are now motivated to generalize Kolmogorov’s result (1.3) to the noncritical case. Let
![]() ${\mathcal{H}}\;:\!=\;\min\{{n\colon Z(n)=0}\}$
be the extinction time of the genealogical tree of one individual. It would be reasonable to call the event
${\mathcal{H}}\;:\!=\;\min\{{n\colon Z(n)=0}\}$
be the extinction time of the genealogical tree of one individual. It would be reasonable to call the event
![]() $\{n<\mathcal{H}<\infty\}$
the bridled-survival condition of the noncritical system. Then we can conclude that under condition (1.4) for the noncritical case the following asymptotic representation holds:
$\{n<\mathcal{H}<\infty\}$
the bridled-survival condition of the noncritical system. Then we can conclude that under condition (1.4) for the noncritical case the following asymptotic representation holds:
where
![]() $\mathcal{K}_q$
is an absolute positive, which can be called the extended Kolmogorov constant. To confirm the assertion (1.6), we first note that the classical extinction theorem implies
$\mathcal{K}_q$
is an absolute positive, which can be called the extended Kolmogorov constant. To confirm the assertion (1.6), we first note that the classical extinction theorem implies
![]() $\mathbb{P}{\{{n<\mathcal{H}<\infty}\mid{Z(n)=k}\}}=q^{k}$
for any
$\mathbb{P}{\{{n<\mathcal{H}<\infty}\mid{Z(n)=k}\}}=q^{k}$
for any
![]() $n\in\mathbb{N}_0$
. Using this, we have
$n\in\mathbb{N}_0$
. Using this, we have
 \begin{align*} Q(n) & = {f_n(q)-f_n(0)} \\[5pt] & = \sum_{k\in\mathcal{S}_0}{P_{1k}(n)q^k}-{P_{11}(n)} = \sum_{k\in\mathcal{S}}\mathbb{P}{\{{n<\mathcal{H}<\infty}, {Z(n)=k}\}} ={\mathbb{P}\{n<\mathcal{H}<\infty\}},\end{align*}
\begin{align*} Q(n) & = {f_n(q)-f_n(0)} \\[5pt] & = \sum_{k\in\mathcal{S}_0}{P_{1k}(n)q^k}-{P_{11}(n)} = \sum_{k\in\mathcal{S}}\mathbb{P}{\{{n<\mathcal{H}<\infty}, {Z(n)=k}\}} ={\mathbb{P}\{n<\mathcal{H}<\infty\}},\end{align*}
which we call the bridled-survival probability of supercritical systems. Next, consider the transformed branching system
![]() $\{Z_{q}(n)\}$
generated by the Harris–Sevastyanov transformation
$\{Z_{q}(n)\}$
generated by the Harris–Sevastyanov transformation
![]() $f_{q}(s)=f(qs)/q$
. This confirms that
$f_{q}(s)=f(qs)/q$
. This confirms that
![]() $\{Z_{q}(n)\}$
is the subcritical BGW system initiated by a single founder-individual whose offspring law is
$\{Z_{q}(n)\}$
is the subcritical BGW system initiated by a single founder-individual whose offspring law is
![]() $\{{q^{k-1}p_k, k\in\mathcal{S}_0}\}$
and whose offspring mean
$\{{q^{k-1}p_k, k\in\mathcal{S}_0}\}$
and whose offspring mean
![]() $\beta={f'(q)}<1$
. Then we can see that
$\beta={f'(q)}<1$
. Then we can see that
![]() $\mathbb{E}Z_{q}(n)=\beta^{n}$
. Further, let
$\mathbb{E}Z_{q}(n)=\beta^{n}$
. Further, let
![]() $f^{(n)}_{q}(s)$
be an n-fold iteration of GF
$f^{(n)}_{q}(s)$
be an n-fold iteration of GF
![]() $f_{q}(s)$
. Therefore, considering the function
$f_{q}(s)$
. Therefore, considering the function
![]() $R^{(q)}_{n}(s)\;:\!=\;1-f^{(n)}_{q}(s)$
as an analogue of
$R^{(q)}_{n}(s)\;:\!=\;1-f^{(n)}_{q}(s)$
as an analogue of
![]() $R_{n}(s)$
, we obtain that
$R_{n}(s)$
, we obtain that
![]() $R_{n}(qs)=qR^{(q)}_{n}(s)$
. Hence, taking
$R_{n}(qs)=qR^{(q)}_{n}(s)$
. Hence, taking
![]() $s=0$
, it follows that
$s=0$
, it follows that
![]() ${\mathbb{P}\{n<\mathcal{H}<\infty\}}=qQ^{(q)}(n)$
, where
${\mathbb{P}\{n<\mathcal{H}<\infty\}}=qQ^{(q)}(n)$
, where
![]() $Q^{(q)}(n)={\mathbb{P}\{{Z_{q}(n)>0}\}}$
. At the same time, according to relation (1.3), we have
$Q^{(q)}(n)={\mathbb{P}\{{Z_{q}(n)>0}\}}$
. At the same time, according to relation (1.3), we have
![]() $Q^{(q)}(n)/{\beta^{n}}\to{K_\beta}$
as
$Q^{(q)}(n)/{\beta^{n}}\to{K_\beta}$
as
![]() $n\to\infty$
, where
$n\to\infty$
, where
![]() ${K_\beta}$
is a positive constant depending on
${K_\beta}$
is a positive constant depending on
![]() $f_{q}(s)$
. So, the desired formula (1.6) is obtained with
$f_{q}(s)$
. So, the desired formula (1.6) is obtained with
![]() $\mathcal{K}_q=q{K}_\beta$
.
$\mathcal{K}_q=q{K}_\beta$
.
Using this notation, we can write out an analogous generalization of Seneta’s result (1.5) in the noncritical case directly from the result of [Reference Imomov9, Lemma 2.1] and formulate it in the following theorem.
Theorem 1.1. Let
![]() $\mathbb{P}\{Z(0)=1\}=1$
and
$\mathbb{P}\{Z(0)=1\}=1$
and
![]() $m\neq{1}$
. Then the bridled-survival probability of the system
$m\neq{1}$
. Then the bridled-survival probability of the system
![]() $\{Z(n)\}$
admits the asymptotic representation
$\{Z(n)\}$
admits the asymptotic representation
![]() ${\mathbb{P}\{{n<{\mathcal{H}}<\infty}\}} = \mathcal{L}_{\beta}({\beta^n}){\beta^{n}}$
as
${\mathbb{P}\{{n<{\mathcal{H}}<\infty}\}} = \mathcal{L}_{\beta}({\beta^n}){\beta^{n}}$
as
![]() $n\to\infty$
, where the function
$n\to\infty$
, where the function
![]() $\mathcal{L}_{\beta}(*)$
varies slowly at zero in the sense of Karamata. If, in addition, condition (1.4) is satisfied, then
$\mathcal{L}_{\beta}(*)$
varies slowly at zero in the sense of Karamata. If, in addition, condition (1.4) is satisfied, then
where
![]() $\{{\mu_k, k\in{\mathcal{S}}}\}$
is a limiting-invariant distribution for the system
$\{{\mu_k, k\in{\mathcal{S}}}\}$
is a limiting-invariant distribution for the system
![]() $\{Z(n)\}$
and has a finite mean
$\{Z(n)\}$
and has a finite mean
![]() $\mu\;:\!=\;{\sum_{k\in{\mathcal{S}}}}{k\mu_{k}}$
such that
$\mu\;:\!=\;{\sum_{k\in{\mathcal{S}}}}{k\mu_{k}}$
such that
Assertion (1.7) implies that the extended Kolmogorov constant
![]() ${{\mathcal{K}_q}}={q/{\mu}}$
, but it can take an explicit form only up to the notation of the limiting-invariant distribution mean. That is, here it is impossible to indicate its dependence on structural parameters, i.e. on the factorial moments of the system offspring distribution.
${{\mathcal{K}_q}}={q/{\mu}}$
, but it can take an explicit form only up to the notation of the limiting-invariant distribution mean. That is, here it is impossible to indicate its dependence on structural parameters, i.e. on the factorial moments of the system offspring distribution.
Thus, our aim in this paper is to get an explicit form of
![]() $\mathcal{K}_q$
.
$\mathcal{K}_q$
.
From now on, we will be accompanied everywhere by the condition
which we call the Kolmogorov condition.
Now we formulate our main result, which explicitly calculates the constant
![]() $\mathcal{K}$
under the Kolmogorov condition (1.8).
$\mathcal{K}$
under the Kolmogorov condition (1.8).
Theorem 1.2. Let the Kolmogorov condition (1.8) be satisfied. Then
![]() $\mathcal{K}_q={q}/({1+q\gamma})$
, where
$\mathcal{K}_q={q}/({1+q\gamma})$
, where
![]() $\gamma={{b_{q}}/{(\beta-\beta^{2})}}$
and
$\gamma={{b_{q}}/{(\beta-\beta^{2})}}$
and
![]() $2b_{q}\;:\!=\;f''(q)$
. In particular, the Kolmogorov constant in the asymptotic formula (1.3) for the subcritical system is
$2b_{q}\;:\!=\;f''(q)$
. In particular, the Kolmogorov constant in the asymptotic formula (1.3) for the subcritical system is
where
![]() $\gamma={{b}/{(m-m^{2})}}$
and
$\gamma={{b}/{(m-m^{2})}}$
and
![]() $2b\;:\!=\;f''(1-)$
.
$2b\;:\!=\;f''(1-)$
.
The rest of the paper is organized as follows. Section 2 we devote to the proof of Theorem 1.2, and in Section 3 we summarize our research and note the main benefits arising from our results.
2. Proof of Theorem 1.2
We divide the proof into several steps.
2.1. Defective but important lemma
Let
![]() ${\textrm{U}_q}[0,1)\;:\!=\;\{[0,q)\cup(q,1)\}$
be a unit interval with a punctured point q. The mean value theorem implies that
${\textrm{U}_q}[0,1)\;:\!=\;\{[0,q)\cup(q,1)\}$
be a unit interval with a punctured point q. The mean value theorem implies that
![]() $q-f(s)=f'({\xi(s)})(q-s)$
for all
$q-f(s)=f'({\xi(s)})(q-s)$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
, where
$s\in{\textrm{U}_q}[0,1)$
, where
![]() ${\xi(s)}=q-(q-s)\theta$
and
${\xi(s)}=q-(q-s)\theta$
and
![]() $\theta\in(0,1)$
. Therefore, iterating over f(s), we write
$\theta\in(0,1)$
. Therefore, iterating over f(s), we write
where
![]() $\xi_n(s)=q-\theta R_n(s)$
. We see that if
$\xi_n(s)=q-\theta R_n(s)$
. We see that if
![]() $s\in[0,q)$
then
$s\in[0,q)$
then
![]() $R_n(s)>0$
, and hence
$R_n(s)>0$
, and hence
![]() $\xi_n(s)<q$
. Since the GF f(s) and its derivatives are monotonically nondecreasing, successive use of the relation (2.1) leads to a uniform upper bound
$\xi_n(s)<q$
. Since the GF f(s) and its derivatives are monotonically nondecreasing, successive use of the relation (2.1) leads to a uniform upper bound
![]() $R_n(s)<q\beta^n$
. Thence,
$R_n(s)<q\beta^n$
. Thence,
![]() $q-q\beta^n<\xi_n(s)<q$
for
$q-q\beta^n<\xi_n(s)<q$
for
![]() $s\in[0,q)$
. Using these relations in (2.1), we obtain the following inequalities:
$s\in[0,q)$
. Using these relations in (2.1), we obtain the following inequalities:
On the other hand,
![]() $R_n(s)<0$
for all
$R_n(s)<0$
for all
![]() $s\in(q,1)$
. This implies that the mean value
$s\in(q,1)$
. This implies that the mean value
![]() $\xi_n(s)=q+\theta\vert{R_n(s)}\vert>q$
. And in this case, successively applying (2.1) and taking into account the monotone nondecreasing property of f’(s), we obtain a uniform lower bound
$\xi_n(s)=q+\theta\vert{R_n(s)}\vert>q$
. And in this case, successively applying (2.1) and taking into account the monotone nondecreasing property of f’(s), we obtain a uniform lower bound
![]() $(q-1)\beta^n<R_n(s)$
or, equivalently,
$(q-1)\beta^n<R_n(s)$
or, equivalently,
![]() $\vert{R_n(s)}\vert <(1-q)\beta^n$
. Hence,
$\vert{R_n(s)}\vert <(1-q)\beta^n$
. Hence,
![]() $q <\xi_n(s)<q+(1-q)\beta^n$
for
$q <\xi_n(s)<q+(1-q)\beta^n$
for
![]() $s\in(q,1)$
. Then
$s\in(q,1)$
. Then
Writing
based on recent results we conclude that
for all
![]() $s\in{\textrm{U}_q}[0,1)$
.
$s\in{\textrm{U}_q}[0,1)$
.
Next, write the Taylor expansion with the Lagrange error bound for f(s):
where
![]() $\zeta(s)$
is the mean value between q and s. Using iteration over f(s) in the last formula gives the following relation:
$\zeta(s)$
is the mean value between q and s. Using iteration over f(s) in the last formula gives the following relation:
where
![]() $\zeta_n(s)$
is the mean value between q and
$\zeta_n(s)$
is the mean value between q and
![]() $f_n(s)$
. Discussions like the previous one confirm that
$f_n(s)$
. Discussions like the previous one confirm that
![]() $q_{0}(n)<\zeta_n(s)< q_{1}(n)$
for all
$q_{0}(n)<\zeta_n(s)< q_{1}(n)$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
. Then, due to the monotonically nondecreasing property of f
′(s),
$s\in{\textrm{U}_q}[0,1)$
. Then, due to the monotonically nondecreasing property of f
′(s),
The combination of (2.4) and (2.5) gives
and, using the estimates (2.3) for only one
![]() $R_n(s)$
on the left and right ends of these inequalities, we transform them to the following form:
$R_n(s)$
on the left and right ends of these inequalities, we transform them to the following form:
Next, multiplying by
![]() ${\beta^{n}}/({R_n(s)R_{n+1}(s)})$
, we rewrite them as
${\beta^{n}}/({R_n(s)R_{n+1}(s)})$
, we rewrite them as
and summing then from 0 to n leads to the following:
 \begin{equation} {\frac{1}{2}}\sum_{k=0}^{n-1}{\frac{f''(q_{0}(k))}{f'(q_{1}(k))}{\beta^{k}}} < {\frac{\beta^{n}}{R_{n}(s)}}-{\frac{1}{q-s}} < {\frac{1}{2}}\sum_{k=0}^{n-1}{\frac{f''(q_{1}(k))}{f'(q_{0}(k))}{\beta^{k}}}.\end{equation}
\begin{equation} {\frac{1}{2}}\sum_{k=0}^{n-1}{\frac{f''(q_{0}(k))}{f'(q_{1}(k))}{\beta^{k}}} < {\frac{\beta^{n}}{R_{n}(s)}}-{\frac{1}{q-s}} < {\frac{1}{2}}\sum_{k=0}^{n-1}{\frac{f''(q_{1}(k))}{f'(q_{0}(k))}{\beta^{k}}}.\end{equation}
Taking the limit as
![]() $n\to\infty$
in (2.6), we have
$n\to\infty$
in (2.6), we have
where
According to (2.2), it follows that
![]() $0<q_{0}(n)<q<q_{1}(n)<1$
for all
$0<q_{0}(n)<q<q_{1}(n)<1$
for all
![]() $n\in\mathbb{N}_{0 }$
. These relations entail that the number series
$n\in\mathbb{N}_{0 }$
. These relations entail that the number series
![]() $\Delta_1$
and
$\Delta_1$
and
![]() $\Delta_2$
converge and
$\Delta_2$
converge and
This leads us to hope that the intermediate term between
![]() ${\Delta_{1}}$
and
${\Delta_{1}}$
and
![]() ${\Delta_{2}}$
in (2.6) approaches
${\Delta_{2}}$
in (2.6) approaches
![]() ${{b_{q}}/{(\beta-\beta^{2})}}$
as
${{b_{q}}/{(\beta-\beta^{2})}}$
as
![]() $n\to\infty$
, which will be proved in Lemma 2.3.
$n\to\infty$
, which will be proved in Lemma 2.3.
Now denoting
we rewrite the relation (2.7) as follows:
Clearly,
![]() ${{1}/{A_2(s)}}-{{1}/{A_1(s)}}={\Delta_2 - \Delta_1}<\infty$
. In turn, we see that
${{1}/{A_2(s)}}-{{1}/{A_1(s)}}={\Delta_2 - \Delta_1}<\infty$
. In turn, we see that
![]() ${{\beta^n}/{R_n(s)}}$
increases for
${{\beta^n}/{R_n(s)}}$
increases for
![]() $s\in[0,q)$
and decreases for
$s\in[0,q)$
and decreases for
![]() $s\in(q,1)$
as
$s\in(q,1)$
as
![]() $n\to\infty$
monotonically. Therefore, in accordance with (2.7), there exists a positive function
$n\to\infty$
monotonically. Therefore, in accordance with (2.7), there exists a positive function
such that
![]() $\Delta(s)\in[\Delta_1, \Delta_2]$
for
$\Delta(s)\in[\Delta_1, \Delta_2]$
for
![]() $s\in{\textrm{U}_q}[0,1)$
.
$s\in{\textrm{U}_q}[0,1)$
.
Thus, we established the following statement.
Lemma 2.1. If the Kolmogorov condition (1.8) is satisfied, then
![]() ${{R_n(s)}/{\beta^{n}}} \longrightarrow {\mathcal{A}_{q}(s)}$
as
${{R_n(s)}/{\beta^{n}}} \longrightarrow {\mathcal{A}_{q}(s)}$
as
![]() $n\to\infty$
for all
$n\to\infty$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
, where
$s\in{\textrm{U}_q}[0,1)$
, where
Note that the pointwise convergence in Lemma 2.1 implies that the function
![]() $\Delta(s)$
is bounded and continuous in
$\Delta(s)$
is bounded and continuous in
![]() $s\in{\textrm{U}_q}[0,1)$
. The principal and only defect of this lemma is the absence of an explicit expression for the function
$s\in{\textrm{U}_q}[0,1)$
. The principal and only defect of this lemma is the absence of an explicit expression for the function
![]() $\Delta(s)$
in (2.8). In Section 2.2 we eliminate this defect.
$\Delta(s)$
in (2.8). In Section 2.2 we eliminate this defect.
2.2. Revelation of
 $\Delta(s)$
and the Q-process contribution
$\Delta(s)$
and the Q-process contribution
The locally asymptotic properties of
![]() $\Delta(s)$
and its derivative will be important in this step. First, we refer to the results of [Reference Athreya and Ney2, Chapter I, §11], where the main properties of the function
$\Delta(s)$
and its derivative will be important in this step. First, we refer to the results of [Reference Athreya and Ney2, Chapter I, §11], where the main properties of the function
![]() $\lim_{n\to\infty}[(f_n(s)-q)/{\beta^{n}}]$
for
$\lim_{n\to\infty}[(f_n(s)-q)/{\beta^{n}}]$
for
![]() $s\in[0,1)$
are established. So, the results from [Reference Athreya and Ney2, p. 40] imply that
$s\in[0,1)$
are established. So, the results from [Reference Athreya and Ney2, p. 40] imply that
![]() $\lim_{n\to\infty}({{R'_n(s)}/{\beta^{n}}})={\mathcal{A}'_{q}(s)}$
exists; furthermore,
$\lim_{n\to\infty}({{R'_n(s)}/{\beta^{n}}})={\mathcal{A}'_{q}(s)}$
exists; furthermore,
but no explicit form of
![]() ${\mathcal{A}'_{q}(s)}$
has been found. Now, transforming (2.8), we write out the following relation:
${\mathcal{A}'_{q}(s)}$
has been found. Now, transforming (2.8), we write out the following relation:
Then, using the assertions in (2.9) and l’Hôpital’s rule in (2.10), we obtain the following important property of
![]() $\Delta(s)$
:
$\Delta(s)$
:
This directly entails that
![]() $\mathcal{A}_{q}(s)\sim{q-s}$
is necessary as
$\mathcal{A}_{q}(s)\sim{q-s}$
is necessary as
![]() $s\to{q}$
.
$s\to{q}$
.
At the same time, it follows from Lemma 2.1 that
![]() $\Delta'(s)$
exists and
$\Delta'(s)$
exists and
for all
![]() $s\in{\textrm{U}_q}[0,1)$
. But this still gives no information on an explicit form of the function
$s\in{\textrm{U}_q}[0,1)$
. But this still gives no information on an explicit form of the function
![]() ${\Delta'(s)}$
. Nevertheless, we see that it is present in the following expression for the derivative of the function
${\Delta'(s)}$
. Nevertheless, we see that it is present in the following expression for the derivative of the function
![]() ${\mathcal{A}_{q}(s)}$
taken directly from (2.8):
${\mathcal{A}_{q}(s)}$
taken directly from (2.8):
This expression will be important later.
Our further discussion is combined with the limiting properties of Q-processes associated with the BGW system
![]() $\{Z(n)\}$
. This system is defined in [Reference Athreya and Ney2, Chapter I, §14] as follows. Consider a probability function
$\{Z(n)\}$
. This system is defined in [Reference Athreya and Ney2, Chapter I, §14] as follows. Consider a probability function
![]() $\mathbb{P}_i^{\mathcal{H}(n+m)}\{*\}\;:\!=\;\mathbb{P}_i\{{\ast\mid{n+m<{\mathcal{H}}<\infty}}\}$
conditioned, in general, on the bridled-survival event for any
$\mathbb{P}_i^{\mathcal{H}(n+m)}\{*\}\;:\!=\;\mathbb{P}_i\{{\ast\mid{n+m<{\mathcal{H}}<\infty}}\}$
conditioned, in general, on the bridled-survival event for any
![]() $m\in{\mathbb{N}}$
of the BGW system. Then, using the ratio limit property of
$m\in{\mathbb{N}}$
of the BGW system. Then, using the ratio limit property of
![]() $P_{ij}(n)$
, it can be calculated that
$P_{ij}(n)$
, it can be calculated that
It is easy to see that
![]() $\{{\mathcal{Q}}_{ij}(n)\}$
is a probability function and determines a new stochastic system called the Q-process. We denote by W(n) the nth time population size. The Q-process is a homogeneous discrete-time Markov chain with state space
$\{{\mathcal{Q}}_{ij}(n)\}$
is a probability function and determines a new stochastic system called the Q-process. We denote by W(n) the nth time population size. The Q-process is a homogeneous discrete-time Markov chain with state space
![]() $\mathcal{E}\subset{\mathbb{N}}$
and n-step transition probabilities
$\mathcal{E}\subset{\mathbb{N}}$
and n-step transition probabilities
for all
![]() $i,j \in {\mathcal{E}}$
. Undoubtedly
$i,j \in {\mathcal{E}}$
. Undoubtedly
![]() $W(0)\mathop=\limits^\mathrm{d} Z(0)$
, and we note that
$W(0)\mathop=\limits^\mathrm{d} Z(0)$
, and we note that
![]() ${\mathcal{Q}}_{ij}(n) = \mathbb{P}_i\{Z(n)=j\mid{\mathcal{H}}=\infty\}$
, so that the Q-process can be interpreted as a ‘long-living’ BGW system. Note also that when the BGW system is aperiodic and irreducible, the Q-process is aperiodic and irreducible in the same sense; see [Reference Athreya and Ney2, pp. 58–59].
${\mathcal{Q}}_{ij}(n) = \mathbb{P}_i\{Z(n)=j\mid{\mathcal{H}}=\infty\}$
, so that the Q-process can be interpreted as a ‘long-living’ BGW system. Note also that when the BGW system is aperiodic and irreducible, the Q-process is aperiodic and irreducible in the same sense; see [Reference Athreya and Ney2, pp. 58–59].
Now consider the GF
![]() $w_n^{(i)}(s)\;:\!=\;\sum_{j\in{\mathcal{E}}} {{\mathcal{Q}}_{ij}(n)s^j}$
. Then, from (1.2) and (2.13), we have
$w_n^{(i)}(s)\;:\!=\;\sum_{j\in{\mathcal{E}}} {{\mathcal{Q}}_{ij}(n)s^j}$
. Then, from (1.2) and (2.13), we have
 \begin{equation*} w_n^{(i)}(s) = \sum\limits_{j \in {\mathcal{E}}} {{\frac{jq^{j-i}}{i\beta^n}}P_{ij}(n)s^j} = {\frac{q^{1-i}s}{i\beta^n}}\sum\limits_{j\in{\mathcal{E}}}{P_{ij}(n)(qs)^{j-1}} = {\frac{qs}{i\beta^n}}{\frac{\partial}{\partial{x}}}\bigg[{\bigg({{\frac{f_n(x)}{q}}}\bigg)^i}\bigg]_{x=qs}. \end{equation*}
\begin{equation*} w_n^{(i)}(s) = \sum\limits_{j \in {\mathcal{E}}} {{\frac{jq^{j-i}}{i\beta^n}}P_{ij}(n)s^j} = {\frac{q^{1-i}s}{i\beta^n}}\sum\limits_{j\in{\mathcal{E}}}{P_{ij}(n)(qs)^{j-1}} = {\frac{qs}{i\beta^n}}{\frac{\partial}{\partial{x}}}\bigg[{\bigg({{\frac{f_n(x)}{q}}}\bigg)^i}\bigg]_{x=qs}. \end{equation*}
The last formula is convenient for use in the following form:
where the GF
![]() $w_n(s)\;:\!=\;w_n^{(1)}(s)=\mathbb{E}{s^{W(n)}}$
has the form
$w_n(s)\;:\!=\;w_n^{(1)}(s)=\mathbb{E}{s^{W(n)}}$
has the form
The use of iteration over f(s) in (2.14) leads to the following functional equation:
where
![]() $w(s)\;:\!=\;w_1(s)$
and
$w(s)\;:\!=\;w_1(s)$
and
![]() $f_{q}(s)= {f(qs)/ q}$
. Thus, the Q-process is completely determined by the GF
$f_{q}(s)= {f(qs)/ q}$
. Thus, the Q-process is completely determined by the GF
The evolution of the Q-process trajectories is essentially regulated by the structural parameter
![]() $\beta >0$
. In fact, as shown in [Reference Athreya and Ney2, p. 59, Theorem 2], if
$\beta >0$
. In fact, as shown in [Reference Athreya and Ney2, p. 59, Theorem 2], if
![]() $\beta <1$
then
$\beta <1$
then
![]() $\mathcal{E}$
is positive recurrent and
$\mathcal{E}$
is positive recurrent and
![]() $\mathcal{E} $
is transient if
$\mathcal{E} $
is transient if
![]() $\beta=1$
. Thus,
$\beta=1$
. Thus,
![]() $\beta \leq{1}$
always and there are no other cases.
$\beta \leq{1}$
always and there are no other cases.
It is easy to be convinced that the positive recurrent case
![]() $\beta <1$
of the Q-process is a defining feature of the noncritical case
$\beta <1$
of the Q-process is a defining feature of the noncritical case
![]() $m\neq{1}$
of the original BGW system. In this case, we assume that
$m\neq{1}$
of the original BGW system. In this case, we assume that
![]() $\alpha\;:\!=\;w'(1-)<\infty$
. Then, differentiating (2.17) at the point
$\alpha\;:\!=\;w'(1-)<\infty$
. Then, differentiating (2.17) at the point
![]() $s=1$
, we obtain
$s=1$
, we obtain
![]() $\alpha=1+({1-\beta})B_{q}$
, where
$\alpha=1+({1-\beta})B_{q}$
, where
It follows from (2.14) and (2.15) that
![]() ${\mathbb{E}}_i W(n)=({i-1})\beta^n+\mathbb{E}W(n)$
, where
${\mathbb{E}}_i W(n)=({i-1})\beta^n+\mathbb{E}W(n)$
, where
![]() $\mathbb{E}W(n)= 1+B_{q}\cdot({1-\beta^n})$
.
$\mathbb{E}W(n)= 1+B_{q}\cdot({1-\beta^n})$
.
Further, it is known [Reference Athreya and Ney2, p. 59, Theorem 2(iv)] that in our case there exists an invariant measure
![]() $\{\pi_j\}$
with respect to the probabilities
$\{\pi_j\}$
with respect to the probabilities
![]() ${{\mathcal{Q} }_{ij}(n)}$
such that
${{\mathcal{Q} }_{ij}(n)}$
such that
where
![]() $\{\nu_{j}\}$
are the coefficients of the power series expansion of
$\{\nu_{j}\}$
are the coefficients of the power series expansion of
![]() $Q(s)=-\mathcal{A}_{q}(s)$
, i.e.
$Q(s)=-\mathcal{A}_{q}(s)$
, i.e.
![]() $\mathcal{A}_{q}(s)=-\sum_{j\in\mathcal{S}_0}{\nu_js^j}$
; see [Reference Athreya and Ney2, p. 41]. Thus, interpreting (2.18) in the context of generating functions, we conclude that there exists a limit function
$\mathcal{A}_{q}(s)=-\sum_{j\in\mathcal{S}_0}{\nu_js^j}$
; see [Reference Athreya and Ney2, p. 41]. Thus, interpreting (2.18) in the context of generating functions, we conclude that there exists a limit function
![]() $\pi(s)\;:\!=\;\sum_{j\in{\mathcal{E}}}{\pi_j s^j}$
such that
$\pi(s)\;:\!=\;\sum_{j\in{\mathcal{E}}}{\pi_j s^j}$
such that
for all
![]() $s\in [0,1)$
. On the other hand, taking the limit as
$s\in [0,1)$
. On the other hand, taking the limit as
![]() $n\to\infty$
in the functional equation (2.16), with a combination of (2.14) and (2.15), leads to the following Schröder-type functional equation:
$n\to\infty$
in the functional equation (2.16), with a combination of (2.14) and (2.15), leads to the following Schröder-type functional equation:
Equation (2.20) entails that
![]() $\pi_j=\sum_{i\in{\mathcal{E}}}{\pi_i{\mathcal{Q}}_{ij}(n)}$
for
$\pi_j=\sum_{i\in{\mathcal{E}}}{\pi_i{\mathcal{Q}}_{ij}(n)}$
for
![]() $n\in{\mathbb{N}}$
and
$n\in{\mathbb{N}}$
and
![]() $j\in{\mathcal{E}}$
.
$j\in{\mathcal{E}}$
.
Now, based on the conclusions made above, we can prove the following statement on more exact behavior of the function
![]() $\Delta(s)$
, which plays the final role on the way to our aim.
$\Delta(s)$
, which plays the final role on the way to our aim.
Lemma 2.2. The function
![]() $\Delta(s)$
is absolutely constant for all
$\Delta(s)$
is absolutely constant for all
![]() $s\in{\textrm{U}_q}[0,1)$
, and
$s\in{\textrm{U}_q}[0,1)$
, and
where
![]() $2b_{q}\;:\!=\;f''(q)$
.
$2b_{q}\;:\!=\;f''(q)$
.
Proof. Considering (2.12), we rewrite (2.19) as follows:
where
We observe that
![]() $\lim_{s\uparrow{1}}M_{q}(s)=1$
, which is immediate due to (2.9) and our notation. Then
$\lim_{s\uparrow{1}}M_{q}(s)=1$
, which is immediate due to (2.9) and our notation. Then
![]() $\pi(1)=1$
, and this argument is equivalent to
$\pi(1)=1$
, and this argument is equivalent to
![]() $\{\pi_j\}$
being an invariant distribution. Differentiating (2.20) with
$\{\pi_j\}$
being an invariant distribution. Differentiating (2.20) with
![]() $s=1$
immediately provides the mean of this distribution:
$s=1$
immediately provides the mean of this distribution:
On the other hand, differentiating (2.22), taking into account the relations (2.8) and (2.23), we first obtain
Then, since
![]() $\pi(1)=1$
, comparing (2.24) and (2.25) leads to the conclusion that it is necessary that
$\pi(1)=1$
, comparing (2.24) and (2.25) leads to the conclusion that it is necessary that
Direct differential calculation of (2.23) gives
 \begin{align} {\frac{\partial{M_q(s)}}{\partial{s}}} & = 2{\mathcal{B}_{q}(s)}{\frac{\mathcal{A}_{q}(qs)}{q(1-s)}}[1+q^{2}(1-s)^{2}\Delta'(qs)] \nonumber \\[5pt] & \quad + \bigg[\frac{\mathcal{A}_{q}(qs)}{q(1-s)}\bigg]^{2} [q^{3}(1-s)^{2}\Delta''(qs)-{2q^{2}(1-s)\Delta'(qs)}], \end{align}
\begin{align} {\frac{\partial{M_q(s)}}{\partial{s}}} & = 2{\mathcal{B}_{q}(s)}{\frac{\mathcal{A}_{q}(qs)}{q(1-s)}}[1+q^{2}(1-s)^{2}\Delta'(qs)] \nonumber \\[5pt] & \quad + \bigg[\frac{\mathcal{A}_{q}(qs)}{q(1-s)}\bigg]^{2} [q^{3}(1-s)^{2}\Delta''(qs)-{2q^{2}(1-s)\Delta'(qs)}], \end{align}
where
and
which is immediate due to (2.8). It follows from (2.12) and (2.28) that
Considering again
![]() $\pi(1)=1$
, from (2.22), (2.23), and (2.28) we obtain that
$\pi(1)=1$
, from (2.22), (2.23), and (2.28) we obtain that
Then combination of (2.11) and (2.27)–(2.30) implies that
as
![]() $s\uparrow{1}$
.
$s\uparrow{1}$
.
To ensure the condition in (2.11), we can now admit all necessary modes of behavior of the variation rate of the function
![]() $\Delta(s)$
as
$\Delta(s)$
as
![]() $s\to{q}$
, which are reduced to the following simple condition:
$s\to{q}$
, which are reduced to the following simple condition:
for all
![]() $s\in{\textrm{U}_q}[0,1)$
, where
$s\in{\textrm{U}_q}[0,1)$
, where
![]() $\sigma\in(\!-\!\infty,1)$
and
$\sigma\in(\!-\!\infty,1)$
and
![]() $\mathcal{L}(\!\ast\!)$
slowly varies at infinity in the sense of Karamata. We prove below that all cases concerning the values of
$\mathcal{L}(\!\ast\!)$
slowly varies at infinity in the sense of Karamata. We prove below that all cases concerning the values of
![]() $\sigma$
, except for the case of
$\sigma$
, except for the case of
![]() $\sigma=0$
, will be forced to be ignored. For this, we first need to estimate the local variation rate of the functions
$\sigma=0$
, will be forced to be ignored. For this, we first need to estimate the local variation rate of the functions
![]() $\Delta'(qs)$
and
$\Delta'(qs)$
and
![]() $\Delta''(qs)$
as
$\Delta''(qs)$
as
![]() $s\uparrow{1}$
in the cases of
$s\uparrow{1}$
in the cases of
![]() $\sigma\neq{0}$
. To do this, we recall that
$\sigma\neq{0}$
. To do this, we recall that
![]() $\mathcal{L}{'}(u)=o(\mathcal{L}(u)/u)$
as
$\mathcal{L}{'}(u)=o(\mathcal{L}(u)/u)$
as
![]() $u\to\infty$
, which is immediate due to the Lamperti theorem [Reference Bingham, Goldie and Teugels3, p. 59]. Using this fact and by the standard differential calculations of (2.32), we have the following relations:
$u\to\infty$
, which is immediate due to the Lamperti theorem [Reference Bingham, Goldie and Teugels3, p. 59]. Using this fact and by the standard differential calculations of (2.32), we have the following relations:
as
![]() $s\to{q}$
. Then, using (2.33) in (2.31), we obtain
$s\to{q}$
. Then, using (2.33) in (2.31), we obtain
For
![]() $\sigma\in(0,1)$
, the term on the right-hand side of (2.34) increases monotonically to infinity as
$\sigma\in(0,1)$
, the term on the right-hand side of (2.34) increases monotonically to infinity as
![]() $s\uparrow{1}$
. This contradicts the boundedness of
$s\uparrow{1}$
. This contradicts the boundedness of
![]() $\Delta(s)$
noted above. In the case of
$\Delta(s)$
noted above. In the case of
![]() $\sigma\in(\!-\!\infty, 0)$
, condition (2.26) cannot be satisfied, since then the limit on the left-hand side of (2.26) would be equal to zero due to (2.34), while
$\sigma\in(\!-\!\infty, 0)$
, condition (2.26) cannot be satisfied, since then the limit on the left-hand side of (2.26) would be equal to zero due to (2.34), while
![]() $B_{q}\neq{0}$
.
$B_{q}\neq{0}$
.
Thus, we have to deal only with the case
![]() $\sigma=0$
, at which
$\sigma=0$
, at which
But the relations (2.10) and (2.12) inevitably lead to the fact that
![]() $\Delta(s)\equiv{\mathrm{constant}}$
. To verify this, let us temporarily assume the opposite, i.e.
$\Delta(s)\equiv{\mathrm{constant}}$
. To verify this, let us temporarily assume the opposite, i.e.
![]() $\mathcal{L}(\!\ast\!)\neq{\mathrm{constant}}$
. Then, once again using the fact that
$\mathcal{L}(\!\ast\!)\neq{\mathrm{constant}}$
. Then, once again using the fact that
![]() $\mathcal{L}{'}(u)=o(\mathcal{L}(u)/u)$
as
$\mathcal{L}{'}(u)=o(\mathcal{L}(u)/u)$
as
![]() $u\to\infty$
, we have
$u\to\infty$
, we have
On the other hand,
![]() $\lim_{s\to{q}}{\mathcal{A}'_{q}(s)}=-1$
and, therefore, (2.10) and (2.12) entail
$\lim_{s\to{q}}{\mathcal{A}'_{q}(s)}=-1$
and, therefore, (2.10) and (2.12) entail
whence
This relation contradicts (2.35) because the right-hand side here converges to 2 as
![]() $s\to{q}$
due to (2.11). The contradiction arose due to the opposite assumption we made that
$s\to{q}$
due to (2.11). The contradiction arose due to the opposite assumption we made that
![]() $\mathcal{L}(\!\ast\!)\neq{\mathrm{constant}}$
. Thus,
$\mathcal{L}(\!\ast\!)\neq{\mathrm{constant}}$
. Thus,
![]() $\Delta(s)\equiv\mathrm{constant}$
for all
$\Delta(s)\equiv\mathrm{constant}$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
. Then
$s\in{\textrm{U}_q}[0,1)$
. Then
![]() $\Delta'(s)=0$
. So, writing
$\Delta'(s)=0$
. So, writing
![]() $\gamma\;:\!=\;\mathcal{L}(u)$
, and taking into account (2.31), our main requirement (2.26) becomes
$\gamma\;:\!=\;\mathcal{L}(u)$
, and taking into account (2.31), our main requirement (2.26) becomes
![]() $2q\gamma = {B_{q}}$
. The assertion (2.21) follows.
$2q\gamma = {B_{q}}$
. The assertion (2.21) follows.
2.3. Basic lemma
Finally, from the representation in (2.8) and the equality in (2.21) we get to an explicit expression for the limit function
![]() $\lim_{n\to\infty}{{R_n(s)}/{\beta^n}}$
that depends on
$\lim_{n\to\infty}{{R_n(s)}/{\beta^n}}$
that depends on
![]() $\beta$
and
$\beta$
and
![]() $b_{q}$
for all
$b_{q}$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
. So, we can now write the following basic lemma, which eliminates the defect of Lemma 2.1 by replacing
$s\in{\textrm{U}_q}[0,1)$
. So, we can now write the following basic lemma, which eliminates the defect of Lemma 2.1 by replacing
![]() $\Delta(s)$
with
$\Delta(s)$
with
![]() $\gamma={B_{q}}/2q$
from Lemma 2.2.
$\gamma={B_{q}}/2q$
from Lemma 2.2.
Lemma 2.3. If the Kolmogorov condition (1.8) is satisfied, then
![]() $R_n(s)={\mathcal{A}_{\gamma}(s)}\beta^n({1+o(1)})$
as
$R_n(s)={\mathcal{A}_{\gamma}(s)}\beta^n({1+o(1)})$
as
![]() $n\to\infty$
for all
$n\to\infty$
for all
![]() $s\in{\textrm{U}_q}[0,1)$
, where
$s\in{\textrm{U}_q}[0,1)$
, where
with
![]() $\gamma={{b_q}/{(\beta-\beta^{2})}}$
and
$\gamma={{b_q}/{(\beta-\beta^{2})}}$
and
![]() $2b_{q}\;:\!=\;f''(q)$
.
$2b_{q}\;:\!=\;f''(q)$
.
Now the primary assertion of the theorem follows directly from Lemma 2.3 as
![]() $s=0$
:
$s=0$
:
Taking
![]() $q=1$
, we obtain (1.9) for the subcritical case. Theorem 1.2 is proved completely.
$q=1$
, we obtain (1.9) for the subcritical case. Theorem 1.2 is proved completely.
3. Concluding remarks
In this final part, we summarize our research and highlight the main achievements.
Remark 3.1. On extra properties of the function
![]() $\mathcal{A}_{\gamma}(s)$
we note that, due to (2.36), it asymptotically satisfies the Schröder functional equation, i.e.
$\mathcal{A}_{\gamma}(s)$
we note that, due to (2.36), it asymptotically satisfies the Schröder functional equation, i.e.
![]() ${\mathcal{A}_{\gamma}({f_n(qs)})}=\beta^n{\mathcal{A}_{\gamma}(qs)}({1+o(1)})$
as
${\mathcal{A}_{\gamma}({f_n(qs)})}=\beta^n{\mathcal{A}_{\gamma}(qs)}({1+o(1)})$
as
![]() $n\to\infty$
for all
$n\to\infty$
for all
![]() $s\in[0,1)$
. These properties are in full compliance with the properties established in [Reference Athreya and Ney2, Chapter I, §11] and also in [Reference Imomov8] for a continuous-time Markov system; see also [Reference Imomov7].
$s\in[0,1)$
. These properties are in full compliance with the properties established in [Reference Athreya and Ney2, Chapter I, §11] and also in [Reference Imomov8] for a continuous-time Markov system; see also [Reference Imomov7].
Remark 3.2. The assertion of Theorem 1.2 contributes to obtaining more information about the invariant measure studied in [Reference Seneta16]. Namely, by virtue of Theorem 1.1 it immediately follows that under the Kolmogorov condition in (1.8), the mean of the limiting-invariant distribution
![]() $\{{\mu_k, k\in\mathcal{S}}\}$
of a noncritical BGW system is
$\{{\mu_k, k\in\mathcal{S}}\}$
of a noncritical BGW system is
where
![]() $\gamma={{b_{q}}/{(\beta-\beta^{2})}}$
and
$\gamma={{b_{q}}/{(\beta-\beta^{2})}}$
and
![]() $2b_{q}\;:\!=\;f''(q)$
.
$2b_{q}\;:\!=\;f''(q)$
.
Remark 3.3. In [Reference Kolmogorov13] and [Reference Nagaev and Badalbaev15] the constant
![]() $\mathcal{K}$
for the subcritical case was defined as
$\mathcal{K}$
for the subcritical case was defined as
![]() $\mathcal{K}=\prod_{k=0}^{\infty}{g(f_k(0))}$
, where
$\mathcal{K}=\prod_{k=0}^{\infty}{g(f_k(0))}$
, where
![]() $g(x)\;:\!=\;[1-f(x)]/[m(1-x)]$
. This completely complies with the explanation in the proof of our theorem. In fact, recalling (1.3) as
$g(x)\;:\!=\;[1-f(x)]/[m(1-x)]$
. This completely complies with the explanation in the proof of our theorem. In fact, recalling (1.3) as
![]() $q=1$
, we write
$q=1$
, we write
 \begin{equation} \mathcal{K}=\lim_{n\to\infty}{\frac{Q(n)}{m^n}} = \lim_{n\to\infty}\prod_{k=0}^{n-1}{\frac{Q(k+1)}{mQ(k)}} = \prod_{k=0}^{\infty}{g(f_k(0))}. \end{equation}
\begin{equation} \mathcal{K}=\lim_{n\to\infty}{\frac{Q(n)}{m^n}} = \lim_{n\to\infty}\prod_{k=0}^{n-1}{\frac{Q(k+1)}{mQ(k)}} = \prod_{k=0}^{\infty}{g(f_k(0))}. \end{equation}
At the same time, (2.1) entails that
 \begin{equation} \mathcal{K} = \lim_{n\to\infty}\prod_{k=0}^{n-1}{\frac{Q(k+1)}{mQ(k)}} = \prod_{k=0}^{\infty}{\frac{f'(\xi_k)}{m}}, \end{equation}
\begin{equation} \mathcal{K} = \lim_{n\to\infty}\prod_{k=0}^{n-1}{\frac{Q(k+1)}{mQ(k)}} = \prod_{k=0}^{\infty}{\frac{f'(\xi_k)}{m}}, \end{equation}
where
![]() $\xi_k\;:\!=\;\xi_k(0)<1$
, and we can see that
$\xi_k\;:\!=\;\xi_k(0)<1$
, and we can see that
![]() ${f'(\xi_k)}/{m}<1$
. According to the arguments of [Reference Nagaev and Badalbaev15] and [Reference Sevastyanov17, Chapter II, §2], the infinite products on the right-hand sides of (3.1) and (3.2) converge provided that the condition (1.4) holds. But this does not suffice to get an explicit form for these, because the convergent series
${f'(\xi_k)}/{m}<1$
. According to the arguments of [Reference Nagaev and Badalbaev15] and [Reference Sevastyanov17, Chapter II, §2], the infinite products on the right-hand sides of (3.1) and (3.2) converge provided that the condition (1.4) holds. But this does not suffice to get an explicit form for these, because the convergent series
![]() $\sum_{k\in{\mathcal{S}}}{p_{k}k\ln{k}}$
does not have an explicit expression depending on offspring moments.
$\sum_{k\in{\mathcal{S}}}{p_{k}k\ln{k}}$
does not have an explicit expression depending on offspring moments.
Remark 3.4. Sometimes, the subcritical GF f(s) can be represented in the form
where
![]() $\upsilon\in(0,1)$
and
$\upsilon\in(0,1)$
and
![]() $L(\!\ast\!)$
slowly varies at infinity in the sense of Karamata. This assumption entails
$L(\!\ast\!)$
slowly varies at infinity in the sense of Karamata. This assumption entails
![]() $\mathbb{E}[Z(1)]^{1+\upsilon}<\infty$
. Then, according to arguments of [Reference Nagaev and Badalbaev15], for the convergence of the products in (3.1) it is necessary and sufficient that the integral
$\mathbb{E}[Z(1)]^{1+\upsilon}<\infty$
. Then, according to arguments of [Reference Nagaev and Badalbaev15], for the convergence of the products in (3.1) it is necessary and sufficient that the integral
be convergent. Results from [Reference Imomov and Kh10, Eq. (2.6)] imply that this integral converges and
where
![]() $L_{0}(t)$
is such that
$L_{0}(t)$
is such that
![]() $L_{0}(t)/L(t)\to{1}$
as
$L_{0}(t)/L(t)\to{1}$
as
![]() $t\to\infty$
. Thereby, the asymptotic behavior of
$t\to\infty$
. Thereby, the asymptotic behavior of
![]() ${{Q(n)}/{m^n}}$
can be observed under a much weaker condition than (1.8). In this case,
${{Q(n)}/{m^n}}$
can be observed under a much weaker condition than (1.8). In this case,
and the problem is directly reduced to calculating the convergent product
But it is apparently impossible to calculate this product explicitly. To do this, the condition in (1.8) should be assumed, which implies that
![]() $\upsilon=1$
and
$\upsilon=1$
and
![]() $L(u)\to{b}$
as
$L(u)\to{b}$
as
![]() $u\to\infty$
. Then we obtain the assertion of Theorem 1.2. Thus, (1.8) is a minimal condition from the viewpoint of the order of the finite offspring moments in this case.
$u\to\infty$
. Then we obtain the assertion of Theorem 1.2. Thus, (1.8) is a minimal condition from the viewpoint of the order of the finite offspring moments in this case.
Remark 3.5. It is especially important to note that our results contribute to the completion of several well-known incomplete limit theorems in the sense of finding an explicit expression for the leading term in asymptotic expansions, which apparently were not explicitly calculated in earlier known works; see, e.g., [Reference Sevastyanov17, Chapter II, §§2, and 4]. So, taking
![]() $s=0$
in Lemma 2.3 immediately leads to the following conclusions in the subcritical case:
$s=0$
in Lemma 2.3 immediately leads to the following conclusions in the subcritical case:
-
(i) If the Kolmogorov condition (1.8) is satisfied, then
where \begin{equation*} m^{-n}{\mathbb{P}\{{\mathcal{H}>n}\}} = {\frac{1}{1+\gamma}}({1+o(1)}) \quad \text{as } n\to\infty, \end{equation*}
\begin{equation*} m^{-n}{\mathbb{P}\{{\mathcal{H}>n}\}} = {\frac{1}{1+\gamma}}({1+o(1)}) \quad \text{as } n\to\infty, \end{equation*}
 $\gamma={{b}/{(m-m^{2})}}$
and
$\gamma={{b}/{(m-m^{2})}}$
and
 $2b\;:\!=\;f''(1-)$
.
$2b\;:\!=\;f''(1-)$
.
-
(ii) Under the Kolmogorov condition (1.8), the expectation of Z(n) on survival trajectories has the asymptotic form
 $\mathbb{E}[Z(n)\mid{\mathcal{H}>n}]=\mu\cdot({1+o(1)})$
as
$\mathbb{E}[Z(n)\mid{\mathcal{H}>n}]=\mu\cdot({1+o(1)})$
as
 $n\to\infty$
, where
$n\to\infty$
, where
 ${\mu=1+\gamma}$
is the limiting-invariant distribution mean of the subcritical BGW system.
${\mu=1+\gamma}$
is the limiting-invariant distribution mean of the subcritical BGW system.
Remark 3.6. A further contribution of Lemma 2.3 is the asymptotic expansion of
![]() ${R'_n(s)}$
, which plays a more important role in the theory of noncritical BGW systems. It follows from the results of [Reference Athreya and Ney2, p. 40, Eq. (9)] that
${R'_n(s)}$
, which plays a more important role in the theory of noncritical BGW systems. It follows from the results of [Reference Athreya and Ney2, p. 40, Eq. (9)] that
![]() $\lim_{n\to\infty}{{R'_n(s)}/{\beta^n}}={\mathcal{A}'_{\gamma}(s)}$
. The following asymptotic relation is then immediate due to the form of (2.36):
$\lim_{n\to\infty}{{R'_n(s)}/{\beta^n}}={\mathcal{A}'_{\gamma}(s)}$
. The following asymptotic relation is then immediate due to the form of (2.36):
for all
![]() $s\in{\textrm{U}_q}[0,1)$
. Therefore, taking
$s\in{\textrm{U}_q}[0,1)$
. Therefore, taking
![]() $s=0$
in (3.3), it directly follows that
$s=0$
in (3.3), it directly follows that
This, combined with the result in [Reference Athreya and Ney2, p. 41, Theorem 3], gives the following improvement of the monotone ratio theorem from [Reference Athreya and Ney2, p. 12]:
(iii) If
![]() $p_1>0$
and the Kolmogorov condition (1.8) is satisfied, then
$p_1>0$
and the Kolmogorov condition (1.8) is satisfied, then
where
![]() $\{\nu_{j},{j\in\mathcal{S}}\}$
are coefficients in the power series expansion of
$\{\nu_{j},{j\in\mathcal{S}}\}$
are coefficients in the power series expansion of
![]() $-\mathcal{A}_{\gamma}(s)$
.
$-\mathcal{A}_{\gamma}(s)$
.
In conclusion, arguments similar to those made in this paper can be used in calculating the constant
![]() $\mathcal{K}_q$
for noncritical continuous-time Markov branching systems in which the second-order moment of the branching rate law is finite. Results on this issue will appear in future work.
$\mathcal{K}_q$
for noncritical continuous-time Markov branching systems in which the second-order moment of the branching rate law is finite. Results on this issue will appear in future work.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.