Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-29T12:37:43.626Z Has data issue: false hasContentIssue false
  • English
  • Français

On the inverse of the first hitting time problem for bidimensional processes

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

Mario Lefebvre
Mario Lefebvre*
Affiliation:
École Polytechnique de Montréal
*
∗Postal address: Département de mathématiques et de génie industriel, École Polytechnique, C. P. 6079, Succursale Centre-ville, Montréal, Québec, Canada H3C 3A7.
Get access Rights & Permissions [Opens in a new window]

Abstract

Bidimensional processes defined by dx(t) = ρ (x, y)dt and dy(t) = m(x, y)dt + [2v(x, y)]1/2dW(t), 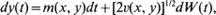where W(t) is a Wiener process, are considered. Let T(x, y) be the first time the process (x(t), y(t)), starting from (x, y), hits the boundary of a given region in 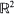. A theorem is proved that gives necessary and sufficient conditions for a given complex function to be considered as the moment generating function of T(x, y) for some bidimensional diffusion process. Examples are given where the theorem is used to construct explicit solutions to first hitting time problems and to compute the infinitesimal moments that correspond to the chosen moment generating function.

Keywords

INTEGRATED PROCESSESHITTING TIMEKOLMOGOROV EQUATION

MSC classification

Primary: 60J70: Applications of Brownian motions and diffusion theory (population genetics, absorption problems, etc.)
Secondary: 60J60: Diffusion processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 3 , September 1997 , pp. 610 - 622
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by the Natural Sciences and Engineering Research Council of Canada and by the fund FCAR of Québec.

References

Abramowitz, M. and Stegun, I. A. (1965) Handbook of Mathematical Functions. Dover, New York.Google Scholar
Arnold, L. (1974) Stochastic Differential Equations: Theory and Applications. Wiley, New York.Google Scholar
Capocelli, R. M. and Ricciardi, L. M. (1972) On the inverse of the first passage time probability problem. J. Appl. Prob. 9, 270–287.CrossRefGoogle Scholar
Feller, W. (1954) Diffusion processes in one dimension. Trans. Amer. Math. Soc. 77, 1–31.CrossRefGoogle Scholar
Fleming, W. H. and Rishel, R. W. (1975) Deterministic and Stochastic Optimal Control. Springer, Berlin.CrossRefGoogle Scholar
Giorno, V., Nobile, A. G. and Ricciardi, L. M. (1988) A new approach to the construction of first-passage-time densities. Cybernet. Syst. 88, 375–381.Google Scholar
Gutiérrez Jáimez, R., Juan Gonzalez, A. and Román Román, P. (1991) Construction of first-passage-time densities for a diffusion process which is not necessarily time-homogeneous. J. Appl. Prob. 28, 903–909.CrossRefGoogle Scholar
Hesse, C. H. (1991) The one-sided barrier problem for an integrated Ornstein-Uhlenbeck process. Commun. Statist.-Stock Models 7, 447–480.CrossRefGoogle Scholar
Iyengar, S. (1985) Hitting lines with a two-dimensional Brownian motion. SIAM J. Appl. Math. 45, 983–989.CrossRefGoogle Scholar
Kannan, D. (1979) An Introduction to Stochastic Processes. North Holland, New York.Google Scholar
Karlin, S. and Taylor, H. (1981) A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
Lachal, A. (1990) Sur l'intégrale du mouvement brownien. C. R. Acad. Sci. Paris Série I Math. 311, 461–464.Google Scholar
Lefebvre, M. (1989a) First-passage densities of a two-dimensional process. SIAM J. Appl. Math. 49, 1514–1523.CrossRefGoogle Scholar
Lefebvre, M. (1989b) Moment generating function of a first hitting place for the integrated Ornstein- Uhlenbeck process. Stoch. Proc. Appl. 32, 281–287.CrossRefGoogle Scholar
Lefebvre, M. (1991a) Forcing a stochastic process to stay in or to leave a given region. Ann. Appl. Prob. 1, 167–172.CrossRefGoogle Scholar
Lefebvre, M. (1991b) Quelques résultats au sujet des densités de premier passage pour des processus de diffusion. Ann. Sci. Math. Québec 15, 165–175.Google Scholar
Lefebvre, M. and Mazigh, M. (1995) Stochastic bargaining models. J. Optim. Theory Appl. 84, 377–391.CrossRefGoogle Scholar
Lefebvre, M. and Whittle, P. (1988) Survival optimization for a dynamic system. Ann. Sci. Math. Québec 12, 101–119.Google Scholar
Rishel, R. (1991) Controlled wear process: modeling optimal control. IEEE Trans. Automat. Cont. 36, 1100–1102.CrossRefGoogle Scholar
Whittle, P. (1982) Optimization over Time. Vol. I. Wiley, Chichester.Google Scholar