Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-22T00:44:23.384Z Has data issue: false hasContentIssue false
  • English
  • Français

On the finiteness and tails of perpetuities under a Lamperti–Kiu MAP

Part of: Stochastic processes Mathematical economics Markov processes

Published online by Cambridge University Press:  22 November 2021

Larbi Alili  and
David Woodford
Larbi Alili*
Affiliation:
University of Warwick
David Woodford*
Affiliation:
University of Warwick
*
*Postal address: The University of Warwick, Coventry CV47AL, UK.
*Postal address: The University of Warwick, Coventry CV47AL, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a Lamperti–Kiu Markov additive process 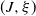$(J, \xi)$ on 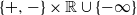$\{+, -\}\times\mathbb R\cup \{-\infty\}$, where J is the modulating Markov chain component. First we study the finiteness of the exponential functional and then consider its moments and tail asymptotics under Cramér’s condition. In the strong subexponential case we determine the subexponential tails of the exponential functional under some further assumptions.

Keywords

Markov additive processLamperti–Kiu representationself-similar Markov processperpetuity

MSC classification

Primary: 60G18: Self-similar processes
Secondary: 60J45: Probabilistic potential theory 91B70: Stochastic models 91B30: Risk theory, insurance
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 1086 - 1113
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alili, L., Chaumont, L., Graczyk, P. and Żak, T. (2017). Inversion, duality and Doob h-transforms for self-similar Markov processes. Electron. J. Prob. 22, 1–18.CrossRefGoogle Scholar
Asmussen, S. (2003). Applied Probability and Queues (Applications of Mathematics: Stochastic Modelling and Applied Probability 51). Springer.Google Scholar
Behme, A. and Sideris, A. (2020). Exponential functionals of Markov additive processes. Electron. J. Prob. 25, 1–25.10.1214/20-EJP441CrossRefGoogle Scholar
Bertoin, J. (1998). Lévy Processes (Camb. Tracts Math). Cambridge University Press.Google Scholar
Bertoin, J. and Yor, M. (2005). Exponential functionals of Lévy processes. Prob. Surveys 2, 191–212.10.1214/154957805100000122CrossRefGoogle Scholar
Carmona, P., Petit, F. and Yor, M. (1994). Sur les fonctionnelles exponentielles de certains processus de Lévy [Exponential functionals of certain Lévy processes]. Stoch. Stoch. Reports 47, 71–101.10.1080/17442509408833883CrossRefGoogle Scholar
Chaumont, L., Pantí, H. and Rivero, V. (2013). The Lamperti representation of real-valued self-similar Markov processes. Bernoulli 19, 2494–2523.10.3150/12-BEJ460CrossRefGoogle Scholar
Cont, R. (2001). Empirical properties of asset returns: stylized facts and statistical issues. Quant. Finance 1, 223–236.CrossRefGoogle Scholar
Embrechts, P. and Hofert, M. (2013). A note on generalized inverses. Math. Methods Operat. Res. 77, 423–432.CrossRefGoogle Scholar
Erickson, K. B. (1973). The strong law of large numbers when the mean is undefined. Trans. Amer. Math. Soc. 185, 371–381.10.1090/S0002-9947-1973-0336806-5CrossRefGoogle Scholar
Foss, S., Korshunov, D. and Zachary, S. (2013). An Introduction to Heavy-Tailed and Subexponential Distributions (Springer Series in Operations Research and Financial Engineering). Springer, New York.10.1007/978-1-4614-7101-1CrossRefGoogle Scholar
Goldie, C. M. (1991). Implicit renewal theory and tails of solutions of random equations. Ann. Appl. Prob. 1, 126–166.10.1214/aoap/1177005985CrossRefGoogle Scholar
Ibragimov, M., Ibragimov, R. and Walden, J. (2015). Heavy-Tailed Distributions and Robustness in Economics and Finance (Lecture Notes Statist. 214). Springer International Publishing.Google Scholar
Jung, R. C. and Liesenfeld, R. (2000). Stochastic volatility models: conditional normality versus heavy-tailed distributions. J. Appl. Econometrics 15, 137–160.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability (Probability Theory and Stochastic Modelling 99). Springer, New York.CrossRefGoogle Scholar
Kesten, H. (1973). Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.CrossRefGoogle Scholar
Kiu, S. W. (1980). Semi-stable Markov processes in $\mathbb{R}^n$. Stoch. Process. Appl. 10, 183–191.CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A. E., Pardo, J. C. and Watson, A. R. (2014). The hitting time of zero for a stable process. Electron. J. Prob. 19, 1–26.CrossRefGoogle Scholar
Lamperti, J. (1962). Semi-stable stochastic processes. Trans. Amer. Math. Soc 104, 62–78.CrossRefGoogle Scholar
Lamperti, J. (1972). Semi-stable Markov processes, I. Z. Wahrscheinlichkeitsth. 22, 205–225.CrossRefGoogle Scholar
Maulik, K. and Zwart, B. (2006). Tail asymptotics for exponential functionals of Lévy processes. Stoch. Process. Appl. 116, 156–177.CrossRefGoogle Scholar
Palau, S., Pardo, J. C. and Smadi, C. (2016). Asymptotic behaviour of exponential functionals of Lévy processes with applications to random processes in random environment. ALEA Lat. Am. J. Prob. Math. Statist. 13, 1235–1258.CrossRefGoogle Scholar
Patie, P. and Savov, M. (2018). Bernstein-gamma functions and exponential functionals of Lévy processes. Electron. J. Prob. 23, 1–101.CrossRefGoogle Scholar
Rachev, S. (2003). Handbook of Heavy Tailed Distributions in Finance (Handbooks in Finance 1). Elsevier Science.Google Scholar
Resnick, S. (2007). Heavy-Tail Phenomena: Probabilistic and Statistical Modeling (Springer Series in Operations Research and Financial Engineering). Springer, New York.Google Scholar
Rivero, V. (2012). Tail asymptotics for exponential functionals of Lévy processes: the convolution equivalent case. Ann. Inst. H. Poincaré Prob. Statist. 48, 1081–1102.CrossRefGoogle Scholar
Stephenson, R. (2018). On the exponential functional of Markov additive processes, and applications to multi-type self-similar fragmentation processes and trees. ALEA Lat. Am. J. Prob. Math. Statist. 15, 1257–1292.10.30757/ALEA.v15-47CrossRefGoogle Scholar
Willekens, E. (1987). On the supremum of an infinitely divisible process. Stoch. Process. Appl. 26, 173–175.10.1016/0304-4149(87)90058-5CrossRefGoogle Scholar
Zachary, S. (2004). A note on Veraverbeke’s theorem. Queueing Systems 46, 9–14.10.1023/B:QUES.0000021155.44510.9fCrossRefGoogle Scholar