Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T07:02:46.909Z Has data issue: false hasContentIssue false
  • English
  • Français

On the determination of a distribution by its median residual life function: a functional equation

Published online by Cambridge University Press:  14 July 2016

Ramesh C. Gupta  and
Eric S. Langford
Ramesh C. Gupta*
Affiliation:
University of Maine at Orono
Eric S. Langford*
Affiliation:
University of Maine at Orono
*
∗ Postal address: Department of Mathematics, University of Maine, Orono, ME 04469, U.S.A.
∗∗ Present address: Department of Mathematics, California State University, Chico, CA 959929–0525, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

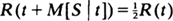In reliability studies, it is well known that the mean residual life function determines the distribution function uniquely. In this paper we show how closely we can determine a distribution when its median residual life function M[S | t] is known. This amounts to solving the functional equation , where R is the reliability function. We actually study a more general functional equation f(φ(t)) = sf(t) called Schroder's equation. It is shown that, under mild assumptions on φ, the solution is of the form f(t) = f0(t)k(log f0 (t)), where f0 is a well-behaved particular solution which can be constructed and k is a periodic function; thus the solution is not unique. Two examples are solved to illustrate the method. Finally, these examples are used to solve the problem of linear M[S | t] studied by Schmittlein and Morrison. As an extra benefit, all of our results hold equally well for the more general sth percentile residual life function.

Keywords

STH PERCENTILE RESIDUAL LIFE FUNCTIONSCHRODER'S FUNCTIONAL EQUATIONRELIABILITY FUNCTIONSLINEAR STH PERCENTILE RESIDUAL LIFE FUNCTIONPARETO DISTRIBUTION
Type
Research Papers
Information
Journal of Applied Probability , Volume 21 , Issue 1 , March 1984 , pp. 120 - 128
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balkema, A. A. and Dehaan, L. (1974) Residual life at great age. Ann. Prob. 2, 792–804.CrossRefGoogle Scholar
Bryson, C. and Siddiqui, M. M. (1969) Some criteria for aging. J. Amer. Statist. Assoc. 64, 1472–1483.Google Scholar
Gertsbakh, I. and Kordonsky, Kh. (1969) Models of Failure. Springer-Verlag, Berlin.CrossRefGoogle Scholar
Gupta, R. C. (1975) On characterization of distributions by conditional expectations. Commun. Statist. 4, 99–103.Google Scholar
Gupta, R. C. (1981) On the mean residual life function in survival studies. In Statistical Distributions in Scientific Work 5, ed. Taillie, C., Patil, G. P. and Baldessari, B. A., Reidel, Dordrecht, 327–334.Google Scholar
Hollander, M. and Proschan, F. (1975) Tests for mean residual life. Biometrika 62, 585–593.Google Scholar
Kuczma, M. (1968) Functional Equations in a Single Variable. Polish Scientific Publishers, Warsaw.Google Scholar
Meilijson, I. (1972) Limiting properties of the mean residual life time function. Ann. Math. Statist. 43, 354–357.CrossRefGoogle Scholar
Muth, E. J. (1977) Reliability models with positive memory derived from the mean residual life function. In Theory and Applications of Reliability, ed. Tsokos, C. P. and Shimi, I. N., Academic Press, New York.Google Scholar
Schmittlein, D. and Morrison, D. (1981) The median residual life time: A characterization theorem and an application. Operat. Res. 29, 392–399.Google Scholar