Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Katori, Makoto
and
Konno, Norio
1991.
Upper bounds for survival probability of the contact process.
Journal of Statistical Physics,
Vol. 63,
Issue. 1-2,
p.
115.
Durrett, R.
1992.
Stochastic growth models: bounds on critical values.
Journal of Applied Probability,
Vol. 29,
Issue. 1,
p.
11.
Neuhauser, Claudia
and
Sudbury, Aidan
1993.
The biased annihilating branching process.
Advances in Applied Probability,
Vol. 25,
Issue. 1,
p.
24.
Liggett, T. M.
1994.
Probability and Phase Transition.
p.
209.
Liggett, Thomas M.
1996.
Multiple transition points for the contact process on the binary tree.
The Annals of Probability,
Vol. 24,
Issue. 4,
Katori, Makoto
1996.
Theory and Applications of the Cluster Variation and Path Probability Methods.
p.
95.
Liggett, Thomas M.
1997.
Stochastic models of interacting systems.
The Annals of Probability,
Vol. 25,
Issue. 1,
Gouet, Raúl
López, F. Javier
and
Sanz, Gerardo
2000.
Estimation of critical values in interacting particle systems.
Journal of Applied Probability,
Vol. 37,
Issue. 1,
p.
118.
Sudbury, Aidan
2000.
The survival of nonattractive interacting particle systems on Z.
The Annals of Probability,
Vol. 28,
Issue. 3,
Gouet, Raúl
López, F. Javier
and
Sanz, Gerardo
2000.
Estimation of critical values in interacting particle systems.
Journal of Applied Probability,
Vol. 37,
Issue. 1,
p.
118.
Sudbury, Aidan
2001.
Rigorous lower bounds for the critical infection rate in the diffusive contact process.
Journal of Applied Probability,
Vol. 38,
Issue. 4,
p.
1074.
Foxall, Eric
2015.
New Results for the Two-Stage Contact Process.
Journal of Applied Probability,
Vol. 52,
Issue. 1,
p.
258.
Foxall, Eric
2015.
New Results for the Two-Stage Contact Process.
Journal of Applied Probability,
Vol. 52,
Issue. 1,
p.
258.
Mu, Y. X.
and
Zhang, Y.
2020.
On some threshold-one attractive interacting particle systems on homogeneous trees.
Journal of Applied Probability,
Vol. 57,
Issue. 3,
p.
866.


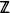 with infection rate
with infection rate 