Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T13:37:00.412Z Has data issue: false hasContentIssue false
  • English
  • Français

On the convergence of the supercritical branching processes with immigration

Published online by Cambridge University Press:  14 July 2016

Harry Cohn
Harry Cohn*
Affiliation:
The Australian National University
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown for a supercritical branching process with immigration that if the log moment 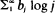of the immigration distribution is infinite, then no sequence of positive constants {cn} exists such that {Xn/cn} converges in law to a proper limit distribution function F, except for the case F(0 +) = 1. Seneta's result [1] combined with the above-mentioned one imply that if 1 < m < ∞ then the finiteness of the log moment of the immigration distribution is a necessary and sufficient condition for the existence of some constants {cn} such that {Xn/cn} converges in law to a proper limit distribution function F, with F(0 +) < 1.

Keywords

BRANCHING PROCESS WITH IMMIGRATIONCONVERGENCE IN DISTRIBUTIONLAW OF LARGE NUMBERS
Type
Short Communications
Information
Journal of Applied Probability , Volume 14 , Issue 2 , June 1977 , pp. 387 - 390
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Seneta, E. (1970) On the supercritical Galton-Watson process with immigration. Math. Biosci. 7, 9–14.Google Scholar
[2] Seneta, E. (1969) Functional equations and the Galton-Watson process. Adv. Appl. Prob. 1, 1–42.Google Scholar