Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hsing, Tailen
1995.
On the asymptotic independence of the sum and rare values of weakly dependent stationary random variables.
Stochastic Processes and their Applications,
Vol. 60,
Issue. 1,
p.
49.
Mathew, G.
and
McCormick, W.P.
1998.
A bootstrap approximation to the joint distribution of sum and maximum of a stationary sequence.
Journal of Statistical Planning and Inference,
Vol. 70,
Issue. 2,
p.
287.
Ho, Hwai-Chung
and
McCormick, William P.
1999.
Asymptotic distribution of sum and maximum for Gaussian processes.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1031.
Ho, Hwai-Chung
and
McCormick, William P.
1999.
Asymptotic distribution of sum and maximum for Gaussian processes.
Journal of Applied Probability,
Vol. 36,
Issue. 4,
p.
1031.
McCormick, W. P.
and
Qi, Y.
2000.
Asymptotic distribution for the sum and maximum of Gaussian processes.
Journal of Applied Probability,
Vol. 37,
Issue. 4,
p.
958.
McCormick, W. P.
and
Qi, Y.
2000.
Asymptotic distribution for the sum and maximum of Gaussian processes.
Journal of Applied Probability,
Vol. 37,
Issue. 4,
p.
958.
Schlather, Martin
2001.
Limit Distributions Of Norms Of Vectors Of Positive I.I.D. Random Variables.
The Annals of Probability,
Vol. 29,
Issue. 2,
Peng, Z.
and
Nadarajah, S.
2003.
On the Joint Limiting Distribution of Sums and Maxima of Stationary Normal Sequence.
Theory of Probability & Its Applications,
Vol. 47,
Issue. 4,
p.
706.
Silvestrov, Dmitrii S.
and
Teugels, Jozef L.
2004.
Limit theorems for mixed max–sum processes with renewal stopping.
The Annals of Applied Probability,
Vol. 14,
Issue. 4,
Ladoucette, Sophie A.
and
Teugels, Jef L.
2007.
Asymptotics for Ratios with Applications to Reinsurance.
Methodology and Computing in Applied Probability,
Vol. 9,
Issue. 2,
p.
225.
James, Barry
James, Kang
and
Qi, Yongcheng
2007.
Limit distribution of the sum and maximum from multivariate Gaussian sequences.
Journal of Multivariate Analysis,
Vol. 98,
Issue. 3,
p.
517.
Dudziński, Marcin
2008.
The almost sure central limit theorems in the joint version for the maxima and sums of certain stationary Gaussian sequences.
Statistics & Probability Letters,
Vol. 78,
Issue. 4,
p.
347.
Wu, Wei Biao
2009.
An asymptotic theory for sample covariances of Bernoulli shifts.
Stochastic Processes and their Applications,
Vol. 119,
Issue. 2,
p.
453.
Hu, Aiping
Peng, Zuoxiang
and
Qi, Yongcheng
2009.
Joint behavior of point process of exceedances and partial sum from a Gaussian sequence.
Metrika,
Vol. 70,
Issue. 3,
p.
279.
Kozubowski, Tomasz J.
Panorska, Anna K.
and
Qeadan, Fares
2011.
A new multivariate model involving geometric sums and maxima of exponentials.
Journal of Statistical Planning and Inference,
Vol. 141,
Issue. 7,
p.
2353.
Tan, Zhong-quan
and
Peng, Zuo-xiang
2011.
Joint asymptotic distribution of exceedances point process and partial sum of stationary Gaussian sequence.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 26,
Issue. 3,
p.
319.
Tan, Zhongquan
and
Wang, Yuebao
2011.
Almost sure central limit theorem for the maxima and sums of stationary Gaussian sequences.
Journal of the Korean Statistical Society,
Vol. 40,
Issue. 3,
p.
347.
PENG, ZUOXIANG
TONG, BIN
and
NADARAJAH, SARALEES
2012.
ALMOST SURE CENTRAL LIMIT THEOREMS OF THE PARTIAL SUMS AND MAXIMA FROM COMPLETE AND INCOMPLETE SAMPLES OF STATIONARY SEQUENCES.
Stochastics and Dynamics,
Vol. 12,
Issue. 03,
p.
1150026.
Weng, Zhichao
Peng, Zuoxiang
and
Nadarajah, Saralees
2012.
The almost sure limit theorem for the maxima and minima of strongly dependent Gaussian vector sequences.
Extremes,
Vol. 15,
Issue. 3,
p.
389.
Qeadan, Fares
Kozubowski, Tomasz J.
and
Panorska, Anna K.
2012.
The Joint Distribution of the Sum and the Maximum of IID Exponential Random Variables.
Communications in Statistics - Theory and Methods,
Vol. 41,
Issue. 3,
p.
544.


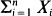 and
and 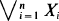 is derived under the condition
is derived under the condition 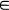 [0,∞). It is seen that the two statistics are asymptotically independent only if
[0,∞). It is seen that the two statistics are asymptotically independent only if 