Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-24T08:06:05.667Z Has data issue: false hasContentIssue false
  • English
  • Français

On random mappings with a single attracting centre

Published online by Cambridge University Press:  14 July 2016

Ljuben R. Mutafchiev
Ljuben R. Mutafchiev*
Affiliation:
Institute of Mathematics, Sofia
*
∗Postal address: Institute of Mathematics, Bulgarian Academy of Sciences, P.O. Box 373, 1090 Sofia, Bulgaria.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the random vector T = (T(0), ···, T(n)) with independent identically distributed coordinates such that Pr{T(i) = j} = Pj, j = 0, 1, ···, n, Σ 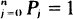. A realization of T can be viewed as a random graph GT with vertices {0, ···, n} and arcs {(0, T(0)), ···, (n, T(n))}. For each T we partition the vertex-set of GT into three disjoint groups and study the joint probability distribution of their cardinalities. Assuming that 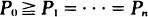we observe the asymptotics of this distribution, as n → ∞, for all possible values of P0. It turns out that in some cases these cardinalities are asymptotically independent and identically distributed.

Keywords

RANDOM GRAPHSLIMITING DISTRIBUTIONS
Type
Short Communications
Information
Journal of Applied Probability , Volume 24 , Issue 1 , March 1987 , pp. 258 - 264
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arney, J. and Bender, E. A. (1982) Random mappings with constraints on coalescence and number of origins. Pacific J. Math. 103, 269–294.Google Scholar
Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
Burtin, Y. D. (1980) On a simple formula for random mappings and its applications. J. Appl. Prob. 17, 403–414.Google Scholar
Jaworski, J. (1984) On a random mapping (T, Pj). J. Appl. Prob. 21, 186–191.Google Scholar
Parthasarathy, K. (1977) Introduction to Probability and Measure. MacMillan Co. of India Ltd., New Delhi.Google Scholar
Ross, S. M. (1981) A random graph. J. Appl. Prob. 18, 309–315.10.2307/3213194Google Scholar
Stepanov, V. E. (1971) Random mappings with a single attracting centre. Theory Prob. Appl. 16, 155–161.10.1137/1116013Google Scholar