Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T19:29:41.478Z Has data issue: false hasContentIssue false
  • English
  • Français

On large-deviation probabilities for the empirical distribution of branching random walks with heavy tails

Part of: Limit theorems Markov processes Stochastic processes

Published online by Cambridge University Press:  24 March 2022

Shuxiong Zhang
Shuxiong Zhang*
Affiliation:
Beijing Normal University
*
*Postal address: School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People’s Republic of China. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a branching random walk 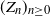$(Z_n)_{n\geq0}$ on 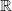$\mathbb{R}$ , let 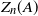$Z_n(A)$ be the number of particles located in interval A at generation n. It is well known that under some mild conditions, 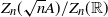$Z_n(\sqrt nA)/Z_n(\mathbb{R})$ converges almost surely to 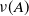$\nu(A)$ as 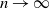$n\rightarrow\infty$ , where $\nu$ is the standard Gaussian measure. We investigate its large-deviation probabilities under the condition that the step size or offspring law has a heavy tail, i.e. a decay rate of 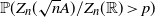$\mathbb{P}(Z_n(\sqrt nA)/Z_n(\mathbb{R})>p)$ as 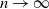$n\rightarrow\infty$ , where 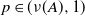$p\in(\nu(A),1)$ . Our results complete those in Chen and He (2019) and Louidor and Perkins (2015).

Keywords

Step sizeoffspring lawSchröder constantCramér’s theorem

MSC classification

Primary: 60F10: Large deviations
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60G50: Sums of independent random variables; random walks
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 2 , June 2022 , pp. 471 - 494
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aïdékon, E., Hu, Y. and Shi, Z. (2019). Large deviations for level sets of branching Brownian motion and Gaussian free fields. J. Math. Sci. 238, 348–365.CrossRefGoogle Scholar
Asmussen, S. and Kaplan, N. (1976). Branching random walks I. Stoch. Process. Appl. 4, 1–13.CrossRefGoogle Scholar
Athreya, K. B. and Hong, J. (2013). An application of the coalescence theory to the branching random walks. J. Appl. Prob. 50, 893–899.CrossRefGoogle Scholar
Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Aurzada, F. (2020). Large deviations for infinite weighted sums of stretched exponential random variables. J. Math. Anal. Appl. 485, 123814.CrossRefGoogle Scholar
Bhattacharya, A. (2018). Large deviation for extremes in branching random walk with regularly varying displacements. Preprint, arXiv:1802.05938.Google Scholar
Biggins, J. D. (1990). The central limit theorem for the supercritical branching random walk, and related results. Stoch. Process. Appl. 34, 255–274,CrossRefGoogle Scholar
Bovier, A. (2016). Gaussian Processes on Trees: From Spin Glasses to Branching Brownian Motion. Cambridge University Press.CrossRefGoogle Scholar
Bramson, M. D., Ding, J. and Zeitouni, O. (2015). Convergence in law of the maximum of the two-dimensional discrete Gaussian free field. Comm. Pure Appl. Math. 69, 62–123.CrossRefGoogle Scholar
Buraczewski, D. and Maślanka, M. (2019). Large deviation estimates for branching random walks. ESAIM Prob. Statist. 23, 823–840.CrossRefGoogle Scholar
Chauvin, B. and Rouault, A. (1988). KPP equation and supercritical branching Brownian motion in the subcritical speed area: Application to spatial trees. Prob. Theory Relat. Fields 80, 299–314.CrossRefGoogle Scholar
Chen, X. (2001). Exact convergence rates for the distribution of particles in branching random walks. Ann. Appl. Prob. 11, 1242–1262.CrossRefGoogle Scholar
Chen, X and He, H. (2019). On large deviation probabilities for empirical distribution of supercritical branching random walks with unbounded displacements. Prob. Theory Relat. Fields 175, 255–307.CrossRefGoogle Scholar
Chen, X. and He, H. (2020). Lower deviation and moderate deviation probabilities for maximum of a branching random walk. Ann. Inst. H. Poincaré Prob. Statist. 56, 2507–2539.CrossRefGoogle Scholar
Dembo, A. and Zeitouni, O. (1998). Large Deviation Techniques and Applications, 2nd edn. Springer, Berlin.CrossRefGoogle Scholar
Denisov, D. E., Korshunov, D. A. and Wachtel, V. I. (2013). On the asymptotics of the tail of distribution of a supercritical Galton–Watson process in the case of heavy tails. Proc. Steklov Inst. Math. 282, 273–297.Google Scholar
Derrida, B. and Shi, Z. (2016). Large deviations for the branching Brownian motion in presence of selection or coalescence. J. Statist. Phys. 163, 1285–1311.CrossRefGoogle Scholar
Derrida, B. and Shi, Z. (2017). Large deviations for the rightmost position in a branching Brownian motion. In Modern Problems of Stochastic Analysis and Statistics. MPSAS 2016, V. Panov (ed.) (Springer Proc. Math. Statist. 208). Springer, Cham.CrossRefGoogle Scholar
Derrida, B. and Shi, Z. (2017). Slower deviations of the branching Brownian motion and of branching random walks. J. Phys. A 50, 344001.CrossRefGoogle Scholar
Fleischmann, K. and Wachtel, V. (2007). Lower deviation probabilities for supercritical Galton–Watson processes. Ann. Inst. H. Poincaré Prob. Statist. 43, 233–255.CrossRefGoogle Scholar
Fleischmann, K. and Wachtel, V. (2008). Large deviations for sums indexed by the generations of a Galton–Watson process. Prob. Theory Relat. Fields 141, 445–470.CrossRefGoogle Scholar
Gantert, N. and Höfelsauer, T. (2018). Large deviations for the maximum of a branching random walk. Electron. Commun. Prob. 23, 1–12.CrossRefGoogle Scholar
Gao, Z. and Liu, Q. (2016). Exact convergence rates in central limit theorems for a branching random walk with a random environment in time. Stoch. Process. Appl. 126, 2634–2664.CrossRefGoogle Scholar
Grübel, R. and Kabluchko, Z. (2017). Edgeworth expansions for profiles of lattice branching random walks. Ann. Inst. H. Poincaré Prob. Statist. 53, 2103–2134.CrossRefGoogle Scholar
Harris, T. E. (1963). The Theory of Branching Processes. Springer, Berlin.CrossRefGoogle Scholar
Hu, Y. (2016). How big is the minimum of a branching random walk? Ann. Inst. H. Poincaré Prob. Statist. 52, 233–260.Google Scholar
Hu, Y. and Shi, Z. (2007). A subdiffusive behaviour of recurrent random walk in random environment on a regular tree. Prob. Theory Relat. Fields 138, 521–549.CrossRefGoogle Scholar
Klebaner, C. F. (1982). Branching random-walk in varying environments. Adv. Appl. Prob. 14, 359–367.CrossRefGoogle Scholar
Liang, X. G. and Liu, Q. (2013). Weighted moments of the limit of a branching process in a random environment. Proc. Steklov Inst. Math. 282, 127–145.CrossRefGoogle Scholar
Liu, Q. (1995). Fixed points of a generalised smoothing transformation and applications to branching processes. Adv. Appl. Prob. 30, 85–112.CrossRefGoogle Scholar
Liu, Q. (2006). On generalised multiplicative cascades. Stoch. Process. Appl. 86, 263–286.CrossRefGoogle Scholar
Louidor, O. and Perkins, W. (2015). Large deviations for the empirical distribution in the branching random walk. Electron. J. Prob. 18, 1–19.Google Scholar
Louidor, O. and Tsairi, E. (2017). Large deviations for the empirical distribution in the general branching random walk. Preprint, arXiv:1704.02374.Google Scholar
Nagaev, S.V. (1979). Large deviations of sums of independent random variables. Ann. Prob., 7, 745–789.CrossRefGoogle Scholar
Ney, P. E. and Vidyashankar, A. N. (2003). Harmonic moments and large deviation rates for supercritical branching processes. Ann. Appl. Prob. 13, 475–489.CrossRefGoogle Scholar
Öz, M. (2020). Large deviations for local mass of branching Brownian motion. ALEA Lat. Am. J. Prob. Math. Statist. 17, 711–731.CrossRefGoogle Scholar
Rouault, A. (1993). Precise estimates of presence probabilities in the branching random walk. Stoch. Process. Appl. 44, 27–39.CrossRefGoogle Scholar
Shi, Z. (2015). Branching Random Walks (Lecture Notes Math. 2151). Springer, Cham.Google Scholar