Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T20:29:52.041Z Has data issue: false hasContentIssue false
  • English
  • Français

On interpoint distances for planar Poisson cluster processes

Published online by Cambridge University Press:  14 July 2016

Richard J. Kryscio  and
Roy Saunders
Richard J. Kryscio*
Affiliation:
University of Kentucky, Lexington
Roy Saunders*
Affiliation:
American Critical Care
*
∗ Postal address: Department of Statistics, University of Kentucky, Lexington, KY 40506, U.S.A. Research carried out while the author was on leave from Northern Illinois University.
∗∗ Postal address: American Critical Care, 1600 Waukegan Road, McGaw Park, IL 60085, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

For stationary Poisson or Poisson cluster processes ξ on R2 we study the distribution of the interpoint distances using the interpoint distance function 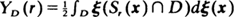and the nearest-neighbor indicator function 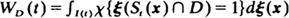. Here Sr (x) is the interior of a circle of radius r having center x, I(t) is that subset of D which has x ∊ D and St(x) ⊂ D and χ is the usual indicator function. We show that if the region D ⊂ R2 is large, then these functions are approximately distributed as Poisson processes indexed by 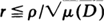and 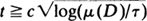, where µ(D) is the Lebesgue measure of D.

Keywords

POINT PROCESSNEAREST-NEIGHBOUR DISTANCEWEAK CONVERGENCETESTS FOR SPATIAL RANDOMNESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 20 , Issue 3 , September 1983 , pp. 513 - 528
Copyright
Copyright © Applied Probability Trust 1983 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Work supported by the National Science Foundation (MCS-79–03781) while both authors were employed by the Department of Mathematical Sciences, Northern Illinois University, DeKalb, IL 60115.

References

Ammann, L. P. and Thall, P. F. (1977) On the structure of regular infinitely divisible point processes. Stoch. Proc. Appl. 6, 87–94.Google Scholar
Billingsley, P. (1968) Weak Convergence of Probability Measures. Wiley, New York.Google Scholar
Conover, W. J. (1972) A Kolmogorov goodness-of-fit test for discontinuous distributions. J. Amer. Statist. Assoc. 67, 591–596.CrossRefGoogle Scholar
Diggle, P. J. (1979) On parameter estimation and goodness-of-fit testing for spatial point patterns. Biometrics 35, 87–101.Google Scholar
Matérn, B. (1960) Spatial variation. Meddlelanden fran Statens Skogsforsksingsinstitut 49, 5.Google Scholar
Neyman, J. (1939) On a new class of contagious distributions, applicable in entomology and bacteriology. Ann. Math. Statist. 10, 35–57.Google Scholar
Neyman, J. and Scott, E. L. (1972) Processes of clustering and applications. In Stochastic Point Processes, ed. Lewis, P. A. W., Wiley, New York, 664–681.Google Scholar
Ripley, B. D. (1977) Modelling spatial patterns. J. R. Statist. Soc. B 39, 172–212.Google Scholar
Ripley, B. D. and Kelly, F. P. (1977) Markov point processes. J. London Math. Soc. 15, 188–192.CrossRefGoogle Scholar
Ripley, B. D. and Silverman, B. W. (1978) Quick tests for spatial interaction. Biometrika 65, 641–642.CrossRefGoogle Scholar
Saunders, R. and Funk, G. M. (1977) Poisson limits for a clustering model of Strauss. J. Appl. Prob. 14, 795–805.Google Scholar
Saunders, R., Kryscio, R. J. and Funk, G. M. (1982) Poisson limits for a hard core clustering model. Stoch. Proc. Appl. 12, 97–106.Google Scholar
Silverman, B. and Brown, T. (1978) Short distances, flat triangles and Poisson limits. J. Appl. Prob. 15, 816–826.Google Scholar
Stoyan, D. (1979) Interrupted point processes. Biom. J. 21, 607–610.Google Scholar
Strauss, D. J. (1975) A model for clustering. Biometrika 62, 467–475.Google Scholar