Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T22:47:43.607Z Has data issue: false hasContentIssue false
  • English
  • Français

On conditional passage time structure of birth-death processes

Published online by Cambridge University Press:  14 July 2016

Ushio Sumita
Ushio Sumita*
Affiliation:
The University of Rochester
*
∗ Postal address: The Graduate School of Management, The University of Rochester, Rochester, NY 14627, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

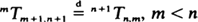Let N(t) be a birth-death process on N = {0,1,2,· ··} governed by the transition rates λn > 0 (n ≧ 0) and μ η > 0 (n ≧ 1). Let mTm be the conditional first-passage time from r to n, given no visit to m where m <r < n. The downward conditional first-passage time nTm is defined similarly. It will be shown that , for any λn > 0 and μ η > 0. The limiting behavior of 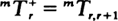is considerably different from that of the ordinary first-passage time 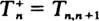where, under certain conditions, exponentiality sets in as n →∞. We will prove that, when λn → λ > 0 and μ η → μ > 0 as n → ∞with ρ = λ /μ < 1, one has 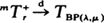as r → ∞where TBP(λ,μ) is the server busy period of an M/M/1 queueing system with arrival rate λand service rate μ.

Keywords

FIRST-PASSAGE TIMESCONDITIONAL FIRST-PASSAGE TIMES
Type
Research Papers
Information
Journal of Applied Probability , Volume 21 , Issue 1 , March 1984 , pp. 10 - 21
Copyright
Copyright © Applied Probability Trust 1984 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was done while the author was at Syracuse University and was published as Working Paper No. 82-001.

References

[1] Callaert, H. and Keilson, J. (1973) On exponential ergodicity and spectral structure for birth-death processes, I. Stoch. Proc. Appl. 1, 187–216.Google Scholar
[2] Callaert, H. and Keilson, J. (1973) On exponential ergodicity and spectral structure for birth-death processes, II. Stoch. Proc. Appl. 1, 217–235.CrossRefGoogle Scholar
[3] Feller, W. (1968) An Introduction to Probability Theory and its Applications, Vol. 1, 3rd edn. Wiley, New York.Google Scholar
[4] Haigh, J. (1978) The asymptotic behavior of a divergent linear birth and death process. J. Appl. Prob. 15, 187–191.CrossRefGoogle Scholar
[5] Hearon, J. Z. (1970) Roots of an irreducible continuant. Linear Algebra Appl. 3, 125–127.CrossRefGoogle Scholar
[6] Karlin, S. and Mcgregor, J. L. (1957) The classification of birth-death processes. Trans. Amer. Math. Soc. 86, 366–400.CrossRefGoogle Scholar
[7] Karlin, S. and Mcgregor, J. L. (1959) A characterization of birth and death processes. Proc. Nat. Acad. Sci. U.S.A. 45, 375–379.CrossRefGoogle ScholarPubMed
[8] Keilson, J. (1964) A review of transient behavior on regular diffusion and birth-death processes, Part I. J. Appl. Prob. 1, 247–266.Google Scholar
[9] Keilson, J. (1965) A review of transient behavior in regular diffusion and birth-death processes, Part II. J. Appl. Prob. 2, 405–428.CrossRefGoogle Scholar
[10] Keilson, J. (1966) A technique for discussing the passage time distribution to stable systems. J. R. Statist. Soc. B 28, 477–486.Google Scholar
[11] Keilson, J. (1971) Log-concavity and log-convexity in passage time densities of diffusion and birth-death processes. J. Appl. Prob. 8, 391–398.Google Scholar
[12] Keilson, J. (1978) Exponential spectra as a tool for the study of server-systems with several classes of customer. J. Appl. Prob. 15, 162–170.CrossRefGoogle Scholar
[13] Keilson, J. (1979) Markov Chain Models — Rarity and Exponentiality. Applied Mathematical Sciences Series 28, Springer-Verlag, Berlin.CrossRefGoogle Scholar
[14] Keilson, J. (1981) On the unimodality of passage time densities in birth–death processes. Statist. Neerlandica 25, 49–55.Google Scholar
[15] Rosenlund, S. I. (1977) Upwards passage times in the non-negative birth–death process. Scand. J. Statist. 4, 90–92.Google Scholar
[16] Rösler, U. (1980) Unimodality of passage time densities for one-dimensional strong Markov processes. Ann. Prob. 8, 853–859.CrossRefGoogle Scholar
[17] Siegel, M. J. (1976) The asymptotic behavior of a divergent birth and death process. Adv. Appl. Prob. 8, 315–338.Google Scholar
[18] Soloviev, A. D. (1972) Asymptotic distribution of the moment of first crossing of a high level by a birth and death process. Proc. 6th Berkeley Symp. Math. Statist. Prob. 3, 71–86.Google Scholar
[19] Tan, W. Y. (1976) On the absorption probabilities and absorption times of finite homogeneous birth-death processes. Biometrics 23, 269–279.Google Scholar
[20] Waugh, W. A. O'N. (1972) Taboo extinction, sojourn times and asymptotic growth for the Markovian birth and death process. J. Appl. Prob. 9, 486–506.CrossRefGoogle Scholar
[21] Williams, T. (1965) The distribution of response times in a birth and death process. Biometrika 52, 581–585.CrossRefGoogle Scholar
[22] Zikun, W. (1980) Sojourn times and first passage times for birth and death processes. Scientia Sinica 23, 269–279.Google Scholar