Article contents
On calculating extinction probabilities for branching processes in random environments
Published online by Cambridge University Press: 14 July 2016
Extract
Consider a discrete time Markov chain {Zn} whose state space is the non-negative integers and whose transition probability matrix ║Pij║ possesses the representation
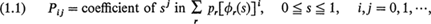 where {Pr}, r = 1,2,…, is a finite or denumerably infinite sequence of non-negative real numbers satisfying
where {Pr}, r = 1,2,…, is a finite or denumerably infinite sequence of non-negative real numbers satisfying 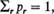 , and
, and 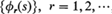 , is a corresponding sequence of probability generating functions. It is assumed that Z0 = k, a finite positive integer.
, is a corresponding sequence of probability generating functions. It is assumed that Z0 = k, a finite positive integer.
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust
References
- 7
- Cited by


