Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T20:34:11.325Z Has data issue: false hasContentIssue false
  • English
  • Français

On a point process with independent locations

Published online by Cambridge University Press:  14 July 2016

Valerie Isham
Valerie Isham*
Affiliation:
Imperial College, London
Get access Rights & Permissions [Opens in a new window]

Abstract

A class of point processes is considered, in which the locations of the points are independent random variables. In particular some properties of the process in which the distribution function of the position of the nth event is the n-fold convolution of some distribution function F, are investigated. It is shown that, under fairly general conditions, the process remote from the origin will be asymptotically Poisson. It is also shown that the variance of the number of events in the interval (0, t] is 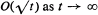. Some generalisations are discussed.

Keywords

INDEPENDENT LOCATIONSCONVOLUTIONSASYMPTOTICALLY POISSONINDEX OF DISPERSIONMULTIDIMENSIONAL POINT PROCESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 12 , Issue 3 , September 1975 , pp. 435 - 446
Copyright
Copyright © Applied Probability Trust 1975 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (1970) Handbook of Mathematical Functions. U.S. National Bureau of Standards.Google Scholar
Çinlar, E. (1972) Superposition of point processes. In Stochastic Point Processes, Ed. Lewis, P. A. W. Wiley, New York.Google Scholar
Daley, D. J. (1971) Some problems in the theory of point processes. Mimeo Series No. 772. University of North Carolina at Chapel Hill, Institute of Statistics.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications. Vol. II. 2nd. edition. Wiley, New York.Google Scholar
Gradshteyn, I. S. and Ryzhik, I. W. (1965) Table of Integrals, Series and Products. Academic Press, New York.Google Scholar