Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T04:23:03.324Z Has data issue: false hasContentIssue false
  • English
  • Français

On a generalization of a waiting time problem and some combinatorial identities

Part of: Combinatorics Sequences and sets Combinatorial probability Polynomials and matrices

Published online by Cambridge University Press:  30 March 2016

B. S. El-desouky ,
F. A. Shiha  and
A. M. Magar
B. S. El-desouky*
Affiliation:
Mansoura University
F. A. Shiha*
Affiliation:
Mansoura University
A. M. Magar*
Affiliation:
Mansoura University
*
∗Postal address: Department of Mathematics, Faculty of Science, Mansoura University, 35516 Mansoura, Egypt.
∗Postal address: Department of Mathematics, Faculty of Science, Mansoura University, 35516 Mansoura, Egypt.
∗Postal address: Department of Mathematics, Faculty of Science, Mansoura University, 35516 Mansoura, Egypt.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we give an extension of the results of the generalized waiting time problem given by El-Desouky and Hussen (1990). An urn contains m types of balls of unequal numbers, and balls are drawn with replacement until first duplication. In the case of finite memory of order k, let ni be the number of type i, i = 1, 2, …, m. The probability of success pi = ni/N, i = 1, 2, …, m, where ni is a positive integer and 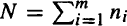Let Ym,k be the number of drawings required until first duplication. We obtain some new expressions of the probability function, in terms of Stirling numbers, symmetric polynomials, and generalized harmonic numbers. Moreover, some special cases are investigated. Finally, some important new combinatorial identities are obtained.

Keywords

Stirling numbergenerating functionwaiting timesymmetric polynomialharmonic number

MSC classification

Primary: 60C05: Combinatorial probability 05A10: Factorials, binomial coefficients, combinatorial functions
Secondary: 05A19: Combinatorial identities, bijective combinatorics 11B73: Bell and Stirling numbers 11C08: Polynomials
Type
Research Papers
Information
Journal of Applied Probability , Volume 52 , Issue 4 , December 2015 , pp. 981 - 989
Copyright
Copyright © Applied Probability Trust 2015 

References

[1] Arnold, B. C. (1972). The waiting time until first duplication. J. Appl. Prob. 9, 841–846.Google Scholar
[2] Beardon, A. F. (1996). Sums of power of integers. Amer. Math. Monthly 103, 201–213.Google Scholar
[3] Cakic, N. P. (1995). The complete Bell polynomials and numbers of Mitrinovic. Univ. Beograd. Publ. Elektrotehn. Fak. Ser. Math. 6, 74–78.Google Scholar
[4] Comtet, L. (1972). Nombres de Stirling généraux et fonctions symétriques. C. R. Acad. Sci. Paris A 275, A747–A750.Google Scholar
[5] Comtet, M. (1974). Advanced Combinatorics. Reidel, Dordrecht.Google Scholar
[6] El-Desouky, B. S. (2015). A generalization of Stirling and Lah numbers with some computational applications. To appear in ARS Combinatoria .Google Scholar
[7] El-Desouky, B. S. and Cakic, N. P. (2011). Generalized higher order Stirling numbers. Math. Comput. Modelling 54, 2848–2857.Google Scholar
[8] El-Desouky, B. S. and Hussen, S. A. (1990). A generalization of a waiting time problem. Adv. Appl. Prob. 22, 758–760.Google Scholar
[9] El-Mikkawy, M. and El-Desouky, B. (2003). On a connection between symmetric polynomials, generalized Stirling numbers and the Newton general divided difference interpolation polynomial. Appl. Math. Comput. 138, 375–385.Google Scholar
[10] Mccabe, B. (1970). Problem E2263. Amer. Math. Monthly 77, 1008.Google Scholar
[11] Riordan, J. (1968). Combinatorial Identities. John Wiley, New York.Google Scholar
[12] Rosen, K. H., (ed.) (2000). Handbook of Discrete and Combinatorial Mathematics. CRC Press, Boca Raton, FL.Google Scholar