Article contents
On a class of random walks in simplexes
Published online by Cambridge University Press: 16 July 2020
Abstract
We study the limit behaviour of a class of random walk models taking values in the standard d-dimensional (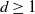 $d\ge 1$
) simplex. From an interior point z, the process chooses one of the
$d\ge 1$
) simplex. From an interior point z, the process chooses one of the 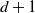 $d+1$
vertices of the simplex, with probabilities depending on z, and then the particle randomly jumps to a new location z′ on the segment connecting z to the chosen vertex. In some special cases, using properties of the Beta distribution, we prove that the limiting distributions of the Markov chain are Dirichlet. We also consider a related history-dependent random walk model in [0, 1] based on an urn-type scheme. We show that this random walk converges in distribution to an arcsine random variable.
$d+1$
vertices of the simplex, with probabilities depending on z, and then the particle randomly jumps to a new location z′ on the segment connecting z to the chosen vertex. In some special cases, using properties of the Beta distribution, we prove that the limiting distributions of the Markov chain are Dirichlet. We also consider a related history-dependent random walk model in [0, 1] based on an urn-type scheme. We show that this random walk converges in distribution to an arcsine random variable.
Keywords
MSC classification
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 2
- Cited by


