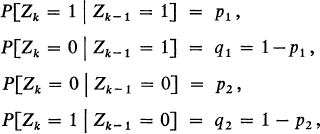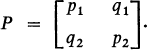Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pedler, P. J.
1980.
Effect of Dependence on the Occupation Time in a Two-State Stationary Markov Chain.
Journal of the American Statistical Association,
Vol. 75,
Issue. 371,
p.
739.
Battaglia, F.
1981.
Upcrossings of discrete hydrologic processes and Markov chains.
Journal of Hydrology,
Vol. 53,
Issue. 1-2,
p.
1.
Bondesson, Lennart
1981.
On occupation times for quasi-Markov processes.
Journal of Applied Probability,
Vol. 18,
Issue. 01,
p.
297.
1983.
Mathematical Techniques of Applied Probability.
p.
231.
Rossiter, M.H.
1989.
THE SOJOURN TIME DISTRIBUTION OF AN ALTERNATING RENEWAL PROCESS.
Australian Journal of Statistics,
Vol. 31,
Issue. 1,
p.
143.
NAIK, VASANTTILAK
1993.
Option Valuation and Hedging Strategies with Jumps in the Volatility of Asset Returns.
The Journal of Finance,
Vol. 48,
Issue. 5,
p.
1969.
Zhang, Hui
and
Knightly, Edward W.
1994.
Providing end-to-end statistical performance guarantees with bounding interval dependent stochastic models.
p.
211.
Clancy, Damian
1994.
Some comparison results for multitype epidemic models.
Journal of Applied Probability,
Vol. 31,
Issue. 1,
p.
9.
Zhang, Hui
and
Knightly, Edward W.
1994.
Providing end-to-end statistical performance guarantees with bounding interval dependent stochastic models.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 22,
Issue. 1,
p.
211.
Lillo, R. E.
1996.
A G/M/1-queue with exponential retrial.
Top,
Vol. 4,
Issue. 1,
p.
99.
Grover, P.
and
Chaturvedi, A.K.
2004.
Upper bounds on the rate of LDPC codes for Gilbert-Elliott channels.
p.
230.
Grover, Pulkit
and
Chaturvedi, Ajit Kumar
2007.
Upper Bounds on the Rate of LDPC Codes for a Class of Finite-State Markov Channels.
IEEE Transactions on Information Theory,
Vol. 53,
Issue. 2,
p.
794.
Kovchegov, Yevgeniy
Meredith, Nick
and
Nir, Eyal
2010.
Occupation times and Bessel densities.
Statistics & Probability Letters,
Vol. 80,
Issue. 2,
p.
104.
Neal, Peter
2012.
The basic reproduction number and the probability of extinction for a dynamic epidemic model.
Mathematical Biosciences,
Vol. 236,
Issue. 1,
p.
31.
Chin, Stephen
and
Dufresne, Daniel
2012.
A General Formula for Option Prices in a Stochastic Volatility Model.
Applied Mathematical Finance,
Vol. 19,
Issue. 4,
p.
313.
Hamidi-Sepehr, Fatemeh
Chamberland, Jean-Francois
and
Pfister, Henry D.
2012.
On the performance of random block codes over finite-state fading channels.
p.
17.
Saunders, David
Seco, Luis
Vogt, Christofer
and
Zagst, Rudi
2013.
A Fund of Hedge Funds Under Regime Switching.
The Journal of Alternative Investments,
Vol. 15,
Issue. 4,
p.
8.
Paroissin, Christian
and
Rabehasaina, Landy
2013.
Statistical Models and Methods for Reliability and Survival Analysis.
p.
369.
Hamidi-Sepehr, Fatemeh
Chamberland, Jean-Francois
and
Pfister, Henry D.
2015.
On the Performance of Block Codes Over Finite-State Channels in the Rare-Transition Regime.
IEEE Transactions on Communications,
Vol. 63,
Issue. 11,
p.
3974.
Chiang, Mi-Hsiu
Li, Chang-Yi
and
Chen, Son-Nan
2016.
Pricing currency options under double exponential jump diffusion in a Markov-modulated HJM economy.
Review of Quantitative Finance and Accounting,
Vol. 46,
Issue. 3,
p.
459.