Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T01:25:27.071Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the selection of random variables under a sum constraint

Published online by Cambridge University Press:  14 July 2016

Wansoo Rhee  and
Michel Talagrand
Wansoo Rhee*
Affiliation:
The Ohio State University
Michel Talagrand*
Affiliation:
Université Paris VI
*
∗ Postal address: Faculty of Management Science, The Ohio State University, 1775 College Road, Columbus, OH 43210, USA.
∗∗ Postal address: Université Paris VI, Equipe d'Analyse, Tour 46, UA au CNRS no. 754, 4 Place Jussieu, 75320 Paris Cedex, France.
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider an i.i.d. sequence of non-negative random variables (X1, · ··, Xn) with known distribution F. Consider decision rules for selecting a maximum number of the 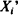subject to the following constraints: (1) the sum of the elements selected must not exceed a given constant c > 0, and (2) the 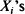must be inspected in strict sequence with the decision to accept or reject an element being final at the time it is inspected. Coffman et al. (1987) proved that there exists such a rule that maximizes the expected number En(c) of variables selected, and determined the asymptotics of En(c) for special distributions. Here we determine the asymptotics of En(cn) for very general choices of sequences (cn) and of F, by showing that En(c) is very close to an easily computable number. Our proofs are (somewhat deceptively) very simple, and rely on an appropriate stopping-time argument.

Keywords

PROPHETTHRESHOLD RULEON-LINE SELECTIONSTOPPING TIME
Type
Short Communications
Information
Journal of Applied Probability , Volume 28 , Issue 4 , December 1991 , pp. 919 - 923
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is also affiliated to the Department of Mathematics, The Ohio State University.

This research was partially supported by an NSF grant.

References

Coffman, E. G., Flatto, L. and Weber, R. R. (1987) Optimal selection of stochastic intervals under a sum constraint. Adv. Appl. Prob. 19, 454–473.10.2307/1427427Google Scholar