Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Speed, T. P.
1973.
A note on random walks. II.
Journal of Applied Probability,
Vol. 10,
Issue. 01,
p.
218.
Kennedy, Douglas P.
1973.
Limit theorems for finite dams.
Stochastic Processes and their Applications,
Vol. 1,
Issue. 3,
p.
269.
Pegg, P. A.
1973.
Some ratio identities for a class of skip free random walks.
Journal of Applied Probability,
Vol. 10,
Issue. 01,
p.
213.
Speed, T. P.
1973.
Some remarks on a result of Blomqvist.
Journal of Applied Probability,
Vol. 10,
Issue. 1,
p.
229.
Phatarfod, R. M.
and
Mardia, K. V.
1973.
Some results for dams with Markovian inputs.
Journal of Applied Probability,
Vol. 10,
Issue. 01,
p.
166.
Barnett, N. S.
1975.
A further note on duality of random walks.
Journal of Applied Probability,
Vol. 12,
Issue. 03,
p.
635.
Tin, Pyke
and
Phatarfod, R. M.
1976.
Some exact results for dams with Markovian inputs.
Journal of Applied Probability,
Vol. 13,
Issue. 02,
p.
329.
Phatarfod, R.M.
1976.
Some aspects of stochastic reservoir theory.
Journal of Hydrology,
Vol. 30,
Issue. 3,
p.
199.
Pegg, P. A.
and
Phatarfod, R. M.
1977.
Dams with additive inputs revisited.
Journal of Applied Probability,
Vol. 14,
Issue. 2,
p.
367.
Imhof, J. P.
1977.
Transactions of the Seventh Prague Conference on Information Theory, Statistical Decision Functions, Random Processes and of the 1974 European Meeting of Statisticians.
p.
277.
Pegg, P. A.
and
Phatarfod, R. M.
1977.
Dams with additive inputs revisited.
Journal of Applied Probability,
Vol. 14,
Issue. 02,
p.
367.
Imhof, J. P.
1978.
One-sided excursions of brownian motion, and an application.
Journal of Applied Probability,
Vol. 15,
Issue. 03,
p.
635.
Phatarfod, Revindra M.
1982.
On some applications of Wald's identity to dams.
Stochastic Processes and their Applications,
Vol. 13,
Issue. 3,
p.
279.
Woolford, Samuel W.
1983.
On a generalized finite-capacity storage model.
Journal of Applied Probability,
Vol. 20,
Issue. 03,
p.
663.
Nozari, Ardavan
Lalli, Janet Carlson
and
Kumin, Hillel
1986.
A random walk approximation for a solar energy storage system.
Solar Energy,
Vol. 37,
Issue. 2,
p.
127.
Abate, Joseph
and
Whitt, Ward
1987.
Transient behavior of regulated Brownian motion, I: Starting at the origin.
Advances in Applied Probability,
Vol. 19,
Issue. 3,
p.
560.
Phatarfod, Ravindra M.
1988.
Sums and weighted sums of a gamma Markov sequence.
Journal of Applied Probability,
Vol. 25,
Issue. 01,
p.
204.
Phatarfod, R. M.
1993.
The geometricity of the limiting distributions in queues and dams.
Journal of Applied Probability,
Vol. 30,
Issue. 02,
p.
438.
Andersen, Lars Nørvang
and
Mandjes, Michel
2009.
Structural properties of reflected Lévy processes.
Queueing Systems,
Vol. 63,
Issue. 1-4,
p.
301.
Andersen, Lars Nørvang
Asmussen, Søren
Glynn, Peter W.
and
Pihlsgård, Mats
2015.
Lévy Matters V.
Vol. 2149,
Issue. ,
p.
67.


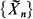 we mean the random walk between absorbing barriers at
we mean the random walk between absorbing barriers at