Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T22:23:14.811Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a condition satisfied by certain random walks

Published online by Cambridge University Press:  14 July 2016

R. A. Doney
R. A. Doney*
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Abstract

The problem considered is to elucidate under what circumstances the condition holds, where 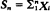and Xi are independent and have common distribution function F. The main result is that if F has zero mean, 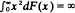and 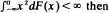(*) holds with 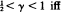F belongs to the domain of attraction of a completely asymmetric stable law of parameter 1/γ. The cases 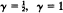are also treated. (The case 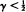cannot arise in these circumstances.) A partial result is also given for the case when 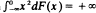and the right-hand tail is ‘asymptotically larger’ than the left-hand tail. For 0 < γ < 1, (*) is known to be a necessary and sufficient condition for the arc-sine theorem to hold for Nn, the number of positive terms in (S1, S2, …, Sn). In the final section we point out that in the case γ = 1 a limit theorem of a rather peculiar type can hold for Nn.

Keywords

RANDOM WALKSARC-SINE THEOREMSTABLE DISTRIBUTIONS
Type
Short Communications
Information
Journal of Applied Probability , Volume 14 , Issue 4 , December 1977 , pp. 843 - 849
Copyright
Copyright © Applied Probability Trust 1977 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bingham, N. H. (1973) Limit theorems in fluctuation theory. Adv. Appl. Prob. 5, 554–569.Google Scholar
[2] Bingham, N. H. and Doney, R. A. (1974) Asymptotic properties of supercritical branching processes I; the Galton-Watson process. Adv. Appl. Prob. 6, 711–731.Google Scholar
[3] Emery, D. J. (1972) Limiting behaviour of the distributions of the maxima of the partial sums of certain random walks. J. Appl. Prob. 9, 572–579.Google Scholar
[4] Emery, D. J. (1975) On a condition satisfied by certain random walks. Z. Wahrscheinlichkeitsth. 31, 125–139.Google Scholar
[5] Heyde, C. C. (1967) Some local limit results in fluctuation theory. J. Austral. Math. Soc. 7, 455–464.Google Scholar
[6] Rogozin, B. A. (1972) The distributions of the first ladder moment and height and fluctuation of a random walk. Theory Prob. Appl. 16, 575–595.Google Scholar
[7] Rosén, B. (1962) On the asymptotic distribution of sums of independent and identically distributed random variables. Ark. Mat. 4, 323–333.Google Scholar
[8] Spitzer, F. (1956) A combinatorial lemma and its application to probability theory. Trans. Amer. Math. Soc. 82, 323–339.Google Scholar
[9] Wolfe, S. J. (1973) On the local behaviour of characteristic functions. Ann. Prob. 1, 862–866.Google Scholar