Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-18T09:44:27.846Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for stability of a bin-packing system

Published online by Cambridge University Press:  24 August 2016

C. Courcoubetis  and
R. R. Weber
C. Courcoubetis*
Affiliation:
AT&T Bell Laboratories
R. R. Weber*
Affiliation:
University of Cambridge
*
∗Postal address: AT&T Bell Laboratories, 600 Mountain Avenue, Murray Hill, NJ 07974, USA.
∗∗Postal address: Queens' College, Cambridge CB3 9ET, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

Objects of various integer sizes, o1, · ··, on, are to be packed together into bins of size N as they arrive at a service facility. The number of objects of size oi which arrive by time t is 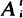, where the components of 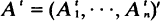are independent renewal processes, with At/t → λ as t → ∞. The empty space in those bins which are neither empty nor full at time t is called the wasted space and the system is declared stabilizable if for some finite B there exists a bin-packing algorithm whose use guarantees the expected wasted space is less than B for all t. We show that the system is stabilizable if the arrival processes are Poisson and λ lies in the interior of a certain convex polyhedral cone Λ. In this case there exists a bin-packing algorithm which stabilizes the system without needing to know λ. However, if λ lies on the boundary of Λ the wasted space grows as 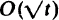and if λ is exterior to Λ it grows as O(t); these conclusions hold even if objects may be repacked as often as desired.

Keywords

ONLINE ALGORITHMSRANDOM WALKSSTOCHASTIC ALGORITHMS
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 4 , December 1986 , pp. 989 - 999
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bentley, J. L., Johnson, D. S., Leighton, F. T., Mcgeoch, C. C. and Mcgeoch, L. A. (1984) Some unexpected results for bin-packing. Bell Laboratories Technical Memorandum.Google Scholar
Coffman, E. G. Jr., Garey, M. R. and Johnson, D. S. (1984) Approximation algorithms for bin-packing — an updated survey, in Algorithm Design for Computer System Design, ed. Ausiello, G., Lucertini, M. and Serafini, P., CISM Courses and Lectures No. 284, Springer-Verlag, New York.Google Scholar
Hoffmann, U. (1982) A class of simple stochastic online bin-packing algorithms. Computing 29, 227–239.Google Scholar