Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tweedie, R. L.
1981.
Criteria for ergodicity, exponential ergodicity and strong ergodicity of Markov processes.
Journal of Applied Probability,
Vol. 18,
Issue. 1,
p.
122.
1982.
The Single Server Queue.
Vol. 8,
Issue. ,
p.
676.
Cocozzathivent, C.
and
Roussignolt, M.
1983.
Stabilite de la recurrence d'une chaine de markov sous i'effet d'une perturbation.
Stochastics,
Vol. 9,
Issue. 1-2,
p.
125.
Cocozza-Thivent, C.
Kipnis, C.
and
Roussignol, M.
1983.
Stabilité de la récurrence nulle pour certaines chaines de Markov perturbées.
Journal of Applied Probability,
Vol. 20,
Issue. 3,
p.
482.
1984.
Markov Chains.
Vol. 11,
Issue. ,
p.
356.
Siegrist, Kyle
1984.
Bivariate step processes and random evolutions.
Journal of Multivariate Analysis,
Vol. 14,
Issue. 2,
p.
201.
Höpfner, Reinhard
1985.
On some classes of population-size-dependent Galton–Watson processes.
Journal of Applied Probability,
Vol. 22,
Issue. 01,
p.
25.
Hanschke, Th.
1985.
The M/G/1/1 queue with repeated attempts and different types of feedback effects.
OR Spektrum,
Vol. 7,
Issue. 4,
p.
209.
Sennott, Linn I.
1987.
Conditions for the non-ergodicity of Markov chains with application to a communication system.
Journal of Applied Probability,
Vol. 24,
Issue. 2,
p.
339.
Ghez, S.
Verdu, S.
and
Schwartz, S.C.
1988.
Stability properties of slotted Aloha with multipacket reception capability.
IEEE Transactions on Automatic Control,
Vol. 33,
Issue. 7,
p.
640.
Malyshev, V. A.
1993.
Networks and dynamical systems.
Advances in Applied Probability,
Vol. 25,
Issue. 1,
p.
140.
Asymont, I. M.
Fayolle, G.
and
Menshikov, Μ. V.
1995.
Random walks in a quarter plane with zero drifts: transience and recurrence.
Journal of Applied Probability,
Vol. 32,
Issue. 4,
p.
941.
Hanschke, T.
1999.
A matrix continued fraction algorithm for the multiserver repeated order queue.
Mathematical and Computer Modelling,
Vol. 30,
Issue. 3-4,
p.
159.
Tweedie, R. L.
2004.
Encyclopedia of Statistical Sciences.
Tweedie, R. L.
2005.
Encyclopedia of Statistical Sciences.
Gonzalez, M.
Molina, M.
and
del Puerto, I.
2006.
Some limit results for controlled branching processes with random control function*.
Journal of Mathematical Sciences,
Vol. 138,
Issue. 1,
p.
5396.
Tweedie, R. L.
2014.
Wiley StatsRef: Statistics Reference Online.
Yu, Jihong
and
Chen, Lin
2015.
Stability analysis of Frame Slotted Aloha protocol.
p.
329.
Spieksma, F.M.
2015.
COUNTABLE STATE MARKOV PROCESSES: NON-EXPLOSIVENESS AND MOMENT FUNCTION.
Probability in the Engineering and Informational Sciences,
Vol. 29,
Issue. 4,
p.
623.
Yu, Jihong
and
Chen, Lin
2017.
Stability Analysis of Frame Slotted Aloha Protocol.
IEEE Transactions on Mobile Computing,
Vol. 16,
Issue. 5,
p.
1462.


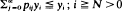 in which
in which 