Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baddeley, Adrian
1977.
Integrals on a moving manifold and geometrical probability.
Advances in Applied Probability,
Vol. 9,
Issue. 3,
p.
588.
Neveu, J.
1977.
Ecole d’Eté de Probabilités de Saint-Flour VI-1976.
Vol. 598,
Issue. ,
p.
249.
Baddeley, Adrian
1977.
A fourth note on recent research in geometrical probability.
Advances in Applied Probability,
Vol. 9,
Issue. 4,
p.
824.
Sheng, T. K.
1985.
The distance between two random points in plane regions.
Advances in Applied Probability,
Vol. 17,
Issue. 4,
p.
748.
Schneider, Rolf
1988.
Random approximation of convex sets*.
Journal of Microscopy,
Vol. 151,
Issue. 3,
p.
211.
Eisenberg, Bennett
and
Sullivan, Rosemary
2000.
Crofton's Differential Equation.
The American Mathematical Monthly,
Vol. 107,
Issue. 2,
p.
129.
Reitzner, Matthias
2004.
Stochastical approximation of smooth convex bodies.
Mathematika,
Vol. 51,
Issue. 1-2,
p.
11.
Moltchanov, D.
2012.
Distance distributions in random networks.
Ad Hoc Networks,
Vol. 10,
Issue. 6,
p.
1146.


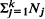 points.
points.