Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Koole, Ger
1993.
Optimal server assignment in the case of service times with monotone failure rates.
Systems & Control Letters,
Vol. 20,
Issue. 3,
p.
233.
Lucantoni, D.M.
Choudhury, G.L.
and
Whitt, W.
1993.
Computing transient distributions in general single-server queues.
p.
1045.
Hordijk, Arie
and
Koole, Ger
1993.
On the optimality of LEPT and μc rules for parallel processors and dependent arrival processes.
Advances in Applied Probability,
Vol. 25,
Issue. 4,
p.
979.
Choudhury, Gagan L.
and
Whitt, Ward
1994.
Heavy-traffic asymptotic expansions for the asymptotic decay rates in theBMAP/G/1 queue.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 2,
p.
453.
Lucantoni, David M.
Choudhury, Gagan L.
and
Whitt, Ward
1994.
The transient BMAP/G/l queue.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 1,
p.
145.
Asmussen, S�ren
and
Bladt, Mogens
1994.
Poisson's equation for queues driven by a Markovian marked point process.
Queueing Systems,
Vol. 17,
Issue. 1-2,
p.
235.
Koole, Ger
1995.
Optimal repairman assignment in two symmetric maintenance models.
European Journal of Operational Research,
Vol. 82,
Issue. 2,
p.
295.
Takine, Tetsuya
and
Hasegawa, Toshiharu
1995.
On the single-server queue with independentMAP/GandM/GIinput streams.
Communications in Statistics. Stochastic Models,
Vol. 11,
Issue. 2,
p.
227.
Akar, Nail
and
Arikan, Erdal
1996.
A numerically efficient method for the MAP/D/1/K queue via rational approximations.
Queueing Systems,
Vol. 22,
Issue. 1-2,
p.
97.
Hordijk, Arie
and
Koole, Ger
1996.
On Suboptimal Policies in Multiclass Tandem Models.
Probability in the Engineering and Informational Sciences,
Vol. 10,
Issue. 1,
p.
29.
Sharma, Vinod
1997.
Approximations of general discrete time queues by discrete time queues with arrivals modulated by finite chains.
Advances in Applied Probability,
Vol. 29,
Issue. 4,
p.
1039.
Koole, Ger
and
Liu, Zhen
1998.
Stochastic Bounds for Queueing Systems with Multiple On–Off Sources.
Probability in the Engineering and Informational Sciences,
Vol. 12,
Issue. 1,
p.
25.
Lucantoni, David
1998.
Further transient analysis of theBMAP/G/1 Queue.
Communications in Statistics. Stochastic Models,
Vol. 14,
Issue. 1-2,
p.
461.
Altman, Eitan
and
Koole, Ger
1998.
On submodular value functions and complex dynamic programming.
Communications in Statistics. Stochastic Models,
Vol. 14,
Issue. 5,
p.
1051.
Takine, Tetsuya
and
Takahashi, Yoshitaka
1998.
On the relationship between queue lengths at a random instant and at a departure in the stationary queue with bmap arrivals.
Communications in Statistics. Stochastic Models,
Vol. 14,
Issue. 3,
p.
601.
Feldmann, Anja
and
Whitt, Ward
1998.
Fitting mixtures of exponentials to long-tail distributions to analyze network performance models.
Performance Evaluation,
Vol. 31,
Issue. 3-4,
p.
245.
Asmussen, Søren
and
Bladt, Mogens
1999.
Point processes with finite-dimensional conditional probabilities.
Stochastic Processes and their Applications,
Vol. 82,
Issue. 1,
p.
127.
Takine, Tetsuya
1999.
The Nonpreemptive Priority MAP/G/1 Queue.
Operations Research,
Vol. 47,
Issue. 6,
p.
917.
Asmussen, Søren
Schmidli, Hanspeter
and
Schmidt, Volker
1999.
Tail probabilities for non-standard risk and queueing processes with subexponential jumps.
Advances in Applied Probability,
Vol. 31,
Issue. 2,
p.
422.
Asmussen, Soren
1999.
Semi-Markov Models and Applications.
p.
269.


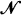 there is a sequence
there is a sequence 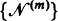 of such Markovian arrival streams with the property that
of such Markovian arrival streams with the property that 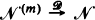 as
as 