Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T11:31:40.049Z Has data issue: false hasContentIssue false
  • English
  • Français

A limit theorem for sample maxima and heavy branches in Galton–Watson trees

Published online by Cambridge University Press:  14 July 2016

G. L. O'brien
G. L. O'brien*
Affiliation:
York University
*
∗Postal address: Department of Mathematics, York University, 4700 Keele St., Downsview, Ontario M3J 1P3, Canada.
Get access Rights & Permissions [Opens in a new window]

Abstract

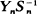Let Yn be the maximum of n independent positive random variables with common distribution function F and let Sn be their sum. Then converges to zero in probability if and only if 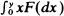is slowly varying. This result implies that in a supercritical Galton-Watson process which does not become extinct, there cannot be a sequence {τ n} of particles, each descended from the preceding one, such that the fraction of all particles which are descendants of τ n does not converge to zero as n →∞. Weakly m-adic trees, which behave to some extent like sample Galton-Watson trees, can have such sequences of particles.

Keywords

SAMPLE MAXIMUMSAMPLE SUMCONVERGENCE IN PROBABILITYSLOW VARIATIONSUPERCRITICAL GALTON-WATSON TREEWEAKLY m -ADIC
Type
Short Communications
Information
Journal of Applied Probability , Volume 17 , Issue 2 , June 1980 , pp. 539 - 545
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by the Natural Sciences and Engineering Research Council of Canada. I am grateful to Cornell University, whose hospitality I enjoyed while working on part of this paper.

References

Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer-Verlag, New York.Google Scholar
Chow, Y. S. and Teicher, H. (1978) Probability Theory: Independence, Interchangeability, Martingales. Springer-Verlag, New York.Google Scholar
Darling, D. A. (1952) The influence of the maximum term in the addition of independent random variables. Trans. Amer. Math. Soc. 73, 95–107.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and its Applications, Vol. 2, 1st edn. Wiley, New York.Google Scholar
Joffe, A. (1978) Remarks on the structure of trees with applications to supercritical Galton-Watson processes. In Advances in Probability 5, ed. Joffe, A. and Ney, P., Dekker, New York, 263–268.Google Scholar
Joffe, A. and Moncayo, A. R. (1973) Random variables, trees and branching random walks. Adv. Math. 10, 401–416.Google Scholar
Kesten, H. (1971) Sums of random variables with infinite expectation. Solution to Advanced Problem #5716. Amer. Math. Monthly 78, 305–308.Google Scholar
Seneta, E. (1974) Regularly varying functions in the theory of simple branching processes. Adv. Appl. Prob. 6, 408–420.Google Scholar