Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T22:40:24.664Z Has data issue: false hasContentIssue false
  • English
  • Français

Laplace ordering and its applications

Published online by Cambridge University Press:  14 July 2016

Abdulhamid Alzaid ,
Jee Soo Kim  and
Frank Proschan
Abdulhamid Alzaid*
Affiliation:
King Saud University
Jee Soo Kim*
Affiliation:
GTE Laboratories
Frank Proschan*
Affiliation:
Florida State University
*
∗Postal address: Department of Statistics, King Saud University, Riyadh 11451, Saudi Arabia.
∗∗Postal address: GTE Laboratories, 40 Sylvan Road, Waltham, MA 02254, USA.
∗∗∗Postal address: Department of Statistics, Florida State University, Tallahassee, FL 32306, USA. Research supported by the Air Force Office of Scientific Research under Grant AFOSR 88–0040.
Get access Rights & Permissions [Opens in a new window]

Abstract

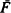Two arbitrary life distributions F and G can be ordered with respect to their Laplace transforms. We say is Laplace-smaller than 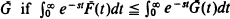for all s > 0. Interpretations of this ordering concept in reliability, operations research, and economics are described. General preservation properties are presented. Using these preservation results we derive useful inequalities and discuss their applications to M/G/1 queues, time series, coherent systems, shock models and cumulative damage models.

Keywords

LAPLACE TRANSFORMSURVIVAL FUNCTIONGENERATING FUNCTIONHNBUERANDOM DAMAGECOMPLETELY MONOTONEQUEUEINGTIME SERIESSERIES SYSTEMPARALLEL SYSTEM
Type
Research Papers
Information
Journal of Applied Probability , Volume 28 , Issue 1 , March 1991 , pp. 116 - 130
Copyright
Copyright © Applied Probability Trust 1991 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Osh, M. and Alzaid, A. A. (1987) First order integer-valued autoregressive (INAR(1)) process. J. Time Series Anal. 8, 261–275.Google Scholar
Abdel-Hameed, M. S. and Proschan, F. (1973) Nonstationary shock models. Stoch. Proc. Appl. 1, 383–404.Google Scholar
Abdel-Hameed, M. S. and Proschan, F. (1975) Shock models with underlying birth process. J. Appl. Prob. 12, 18–28.Google Scholar
Barlow, R. E. and Proschan, F. (1981) Statistical Theory of Reliability and Life Testing: Probability Models. To Begin With, Silver Spring, MD.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and Its Applications, Vol. II. Wiley, New York.Google Scholar
K?Mi?N, M. I. and Schwartz, N. L. (1981) Dynamic Optimization: The Calculus of Variation and Optimal Control in Economics and Management. North-Holland, New York.Google Scholar
Klefsjö, B. (1981) HNBUE survival under some shock models. Scand. J. Statist. 8, 39–47.Google Scholar
Klefsjö, B. (1983) A useful ageing property based on the Laplace transform J. Appl. Prob. 20, 615–626.Google Scholar
Lawrance, A. J. and Lewis, P. A. W. (1985) Modeling and residual analysis of non-linear autoregressive time series n-exponential variables (with discussion). J. R. Statist. Soc. B47, 165–202.Google Scholar
Råde, L. (1972) On the use of generating functions and Laplace transforms in applied probability theory. Internat. J. Math. Educ. Sci. Technol. 3, 25–33.Google Scholar
Rolski, T. and Stoyan, D. (1976) On the comparison of waiting times in GI/G/1 queues. Operat. Res. 24, 197–199.CrossRefGoogle Scholar
Ross, S. M. and Schechner, Z. (1984) Some reliability applications of the variability ordering. Operat. Res. 32, 679–687.Google Scholar
Saaty, T. L. (1961) Elements of Queueing Theory With Applications. McGraw-Hill, New York.Google Scholar
Stoyan, D. (1983) Comparison Models For Queues and Other Stochastic Models. Wiley, New York.Google Scholar
Widder, D. V. (1946) The Laplace Transform. Princeton University Press.Google Scholar