Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T10:58:47.384Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite divisibility of infinite sums of lower records: a simple proof

Part of: Distribution theory - Probability

Published online by Cambridge University Press:  14 July 2016

Aleksander M. Iksanov
Aleksander M. Iksanov*
Affiliation:
Taras Shevchenko National University of Kiev
*
∗ Postal address: Faculty of Cybernetics, Taras Shevchenko National University of Kiev, 01033 Kiev, Ukraine. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {X n , n = 0, 1,…} be the sequence of the lower records for an arbitrary underlying distribution μ on [0, ∞). We show that 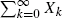is equal in distribution to 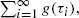where {τ i , i = 1, 2,…} is a Poisson flow of unit intensity and g is a right-continuous and nonincreasing function defined by μ. This observation allows us to extend results of Bose et al. and simplify their proofs.

Keywords

Lower recordinfinite divisibilityshot noise distribution

MSC classification

Primary: 60E07: Infinitely divisible distributions; stable distributions 60E10: Characteristic functions; other transforms
Type
Short Communications
Information
Journal of Applied Probability , Volume 41 , Issue 4 , December 2004 , pp. 1187 - 1190
Copyright
Copyright © Applied Probability Trust 2004 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bose, A., Gangopadhyay, S., Sarkar, A., and Sengupta, A. (2003). Convergence of lower records and infinite divisibility. J. Appl. Prob. 40, 865–880.CrossRefGoogle Scholar
Bose, A., Gangopadhyay, S., Sarkar, A., and Sengupta, A. (2003). Asymptotic properties of sums of upper records. Extremes 6, 147–164.CrossRefGoogle Scholar
Bunge, J., and Goldie, C. M. (2001). Record sequences and their applications. In Handbook of Statistics, Vol. 19, Stochastic Processes: Theory and Methods, eds Shanbhag, D. N. and Rao, C. R., North-Holland, Amsterdam, pp. 277–308.Google Scholar
Iksanov, A. M., and Jurek, Z. J. (2003). Shot noise distributions and selfdecomposability. Stoch. Anal. Appl. 21, 593–609.CrossRefGoogle Scholar
Szekli, R. (1995). Stochastic Ordering and Dependence in Applied Probability (Lecture Notes Statist. 97). Springer, New York.Google Scholar
Vervaat, W. (1979). On a stochastic difference equation and a representation of nonnegative infinitely divisible random variables. Adv. Appl. Prob. 11, 750–783.CrossRefGoogle Scholar