Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Autar, Ram
and
Soni, R. S.
1976.
Generalized inaccuracy and a coding theorem.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 84,
Issue. 5,
p.
204.
Dial, Gur
1987.
On Non-Additive Measures of Inaccuracy and A Coding Theorem.
Journal of Information and Optimization Sciences,
Vol. 8,
Issue. 1,
p.
113.
Bhatia, P.K.
Taneja, H.C.
and
Tuteja, R.K.
1993.
Inaccuracy and the best 1:1 code.
Microelectronics Reliability,
Vol. 33,
Issue. 6,
p.
905.
Hooda, D. S.
and
Ram, Anant
1998.
Bounds onL
Β1:1(t) in terms of a generalized measure of entropy.
Korean Journal of Computational & Applied Mathematics,
Vol. 5,
Issue. 1,
p.
201.


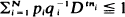 .
.