Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T10:04:01.923Z Has data issue: false hasContentIssue false
  • English
  • Français

The geometric convergence rate of a Lindley random walk

Part of: Markov processes Special processes

Published online by Cambridge University Press:  14 July 2016

Robert B. Lund
Robert B. Lund*
Affiliation:
University of Georgia
*
∗Postal address: Department of Statistics, The University of Georgia, Athens, GA 30602–1952, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {Xn} be the Lindley random walk on [0,∞) defined by 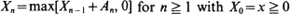. Here, {An} is a sequence of independent and identically distributed random variables. When 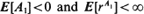for some r > 1, {Xn} converges at a geometric rate in total variation to an invariant distribution π; i.e. there exists s > 1 such that for every initial state 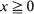. In this communication we supply a short proof and some extensions of a large deviations result initially due to Veraverbeke and Teugels (1975, 1976): the largest s satisfying the above relationship is and 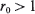satisfies φ ‘(r0) = 0.

Keywords

MARKOV CHAINGEOMETRIC CONVERGENCETOTAL VARIATIONQUEUES

MSC classification

Primary: 60K25: Queueing theory
Secondary: 60J25: Continuous-time Markov processes on general state spaces
Type
Short Communications
Information
Journal of Applied Probability , Volume 34 , Issue 3 , September 1997 , pp. 806 - 811
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Afanas'Ev, V. I. (1979) A conditional random walk with negative drift. Theory Prob. Appl. 24, 192–197.CrossRefGoogle Scholar
[2] Asmussen, S. (1987) Applied Probability and Queues. Wiley, New York.Google Scholar
[3] Bahadur, R. R. and Rao, R. R. (1960) On deviations of the sample mean. Ann. Math. Statist. 31, 1015–1027.CrossRefGoogle Scholar
[4] Chernoff, H. (1952) A measure of asymptotic efficiency for test of a hypothesis based on the sum of observations. Ann. Math. Statist. 23, 493–507.CrossRefGoogle Scholar
[5] Cohen, J. W. (1982) The Single Server Queue. Revised edition. North-Holland, Amsterdam.Google Scholar
[6] Lund, R. B. and Tweedie, R. L. (1996) Geometric convergence rates for stochastically ordered Markov chains. Math. Operat. Res. 20, 182–194.CrossRefGoogle Scholar
[7] Prabhu, N. U. (1980) Stochastic Storage Models. Springer, New York.CrossRefGoogle Scholar
[8] Veraverbeke, N. and Teugels, J. L. (1975) The exponential rate of convergence of the disttribution of the maximum of a random walk. J. Appl. Prob. 12, 279–288.Google Scholar
[9] Veraverbeke, N. and Teugels, J. L. (1976) The exponential rate of convergence of the distribution of the maximum of a random walk. Part II. J. Appl. Prob. 13, 733–740.Google Scholar