Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T07:12:29.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed Precision MCMC Estimation by Median of Products of Averages

Part of: Probabilistic methods, simulation and stochastic differential equations Equilibrium statistical mechanics Algorithms - Computer Science Markov processes

Published online by Cambridge University Press:  14 July 2016

Wojciech Niemiro  and
Piotr Pokarowski
Wojciech Niemiro*
Affiliation:
Nicolaus Copernicus University
Piotr Pokarowski*
Affiliation:
University of Warsaw
*
∗Work partially supported by the Polish Ministry of Science and Higher Education (grant number N N201 387234).
∗Work partially supported by the Polish Ministry of Science and Higher Education (grant number N N201 387234).
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The standard Markov chain Monte Carlo method of estimating an expected value is to generate a Markov chain which converges to the target distribution and then compute correlated sample averages. In many applications the quantity of interest θ is represented as a product of expected values, θ = µ1 ⋯ µk, and a natural estimator is a product of averages. To increase the confidence level, we can compute a median of independent runs. 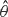The goal of this paper is to analyze such an estimator , i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for 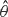to have fixed relative precision at a given level of confidence, that is, to satisfy 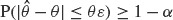. Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.

Keywords

Markov chain Monte Carlorare-event simulationmean-square errorbiasconfidence estimation

MSC classification

Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces) 65C05: Monte Carlo methods 68W20: Randomized algorithms 82B80: Numerical methods (Monte Carlo, series resummation, etc.)
Type
Research Article
Information
Journal of Applied Probability , Volume 46 , Issue 2 , June 2009 , pp. 309 - 329
Copyright
Copyright © Applied Probability Trust 2009 

References

[1] Aldous, D. (1987). On the Markov chain simulation method for uniform combinatorial distributions and simulated annealing. Prob. Eng. Inf. Sci. 1, 33–46.Google Scholar
[2] Asmussen, S. (2000). Ruin Probabilities (Adv. Ser. Statist. Sci. Appl. Prob. 2). World Scientific, River Edge, NJ.CrossRefGoogle Scholar
[3] Asmussen, S. and Binswanger, K. (1997). Simulation of ruin probabilities for subexponential claims. ASTIN Bull. 27, 297–318.Google Scholar
[4] Asmussen, S. and Glynn, P. W. (2007). Stochastic Simulation: Algorithms and Analysis (Stoch. Modelling Appl. Prob. 57). Springer, New York.Google Scholar
[5] Asmussen, S. and Kroese, D. P. (2006). Improved algorithms for rare event simulation with heavy tails. Adv. Appl. Prob. 38, 545–558.Google Scholar
[6] Bernstein, S. N. (1924). On a modification of Chebyshev's inequality and of the error formula of Laplace. Ann. Sci. Inst. Savantes Ukraine, Sect. Math. 1, 38–49.Google Scholar
[7] Bremaud, P. (1999). Markov Chains. Springer, New York.Google Scholar
[8] Diaconis, P. and Strook, D. (1991). {Geometric bounds for eigenvalues of Markov chains}. Ann. Appl. Prob. 1, 36–61.Google Scholar
[9] Diaconis, P., Holmes, S. and Neal, R. M. (2000). Analysis of a nonreversible Markov chain sampler. Ann. Appl. Prob. 10, 726–752.Google Scholar
[10] Dinwoodie, I. H. (1995). A probability inequality for the occupation measure of a reversible Markov chain. Ann. Appl. Prob. 5, 37–43.Google Scholar
[11] Dyer, M. and Frieze, A. (1991). {Computing the volume of convex bodies: a case where randomness provably helps}. In Probabilistic Combinatorics and its Applications (Proc. AMS Symp. Appl. Math. 44), American Mathematical Society, Providence, RI, pp. 123–169.Google Scholar
[12] Dyer, M., Goldberg, L. A. and Jerrum, M. (2006). Systematic scan for sampling colorings. Ann. Appl. Prob. 16, 185–230.Google Scholar
[13] Ferrenberg, A. M. and Swendsen, R. H. (1989). Optimized Monte Carlo data analysis. Phys. Rev. Lett. 63, 1195–1198.Google Scholar
[14] Fill, J. A. (1991). Eigenvalue bounds on convergence to stationarity for nonreversible Markov chains, with an application to the exclusion process. Ann. Appl. Prob. 1, 62–87.CrossRefGoogle Scholar
[15] Gillman, D. (1998). A Chernoff bound for random walks on expander graphs. SIAM J. Comput. 27, 1203–1220.Google Scholar
[16] Hartinger, J. and Kortschak, D. (2006). On the efficiency of Asmussen–Kroese-estimator and its applications to stop-loss transforms. In 6th Internat. Workshop on Rare Event Simulation (Bamberg, October 2006), pp. 162–171.Google Scholar
[17] Hoeffding, W. (1963). Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58, 13–30.CrossRefGoogle Scholar
[18] Horn, R. and Johnson, C. R. (1985). Matrix Analysis. Cambridge University Press.Google Scholar
[19] Jerrum, M. (2003). Counting, Sampling and Integrating: Algorithms and Complexity, Birkhäuser, Basel.CrossRefGoogle Scholar
[20] Jerrum, M. and Sinclair, A. (1993). Polynomial-time approximation algorithms for the Ising model. SIAM. J. Comput. 22, 1087–1116.CrossRefGoogle Scholar
[21] Jerrum, M. and Sinclair, A. (1996). {The Markov chain Monte Carlo method: an approach to approximate counting and integration}, In Approximation Algorithms for NP-hard Problems, ed. Hochbaum, D., PWS, Boston, pp. 482–520.Google Scholar
[22] Jerrum, M., Sinclair, A. and Vigoda, E. (2004). A polynomial-time approximation algorithm for the permanent of a matrix with nonnegative entries. J. Assoc. Comput. Mach. 51, 671–697.Google Scholar
[23] Jerrum, M. R., Valiant, L. G. and Vazirani, V. V. (1986). Random generation of combinatorial structures from a uniform distribution. Theoret. Comput. Sci. 43, 169–188.CrossRefGoogle Scholar
[24] Lezaud, P. (1998). Chernoff-type bound for finite Markov chains. Ann. Appl. Prob. 8, 849–867.CrossRefGoogle Scholar
[25] Niemiro, W. (2008). Nonasymptotic bounds on the estimation error for regenerative MCMC algorithm under a drift condition. Submitted.Google Scholar
[26] Newman, M. E. J. and Barkema, G. T. (1999). Monte Carlo Methods in Statistical Physics. Clarendon Press, New York.CrossRefGoogle Scholar
[27] Pokarowski, P., Droste, K. and Kolinski, A. (2005). A minimal protein-like lattice model: an alpha-helix motif. J. Chem. Phys. 122, 214915.CrossRefGoogle Scholar
[28] Pokarowski, P., Kolinski, A. and Skolnick, J. (2003). A minimal physically realistic protein-like lattice model: designing an energy landscape that ensures all-or-none folding to a unique native state. Biophysical J. 84, 1518–1526.Google Scholar
[29] Sandman, W. (ed.) (2006). Proceedings of the 6th International Workshop on Rare Event Simulation (Bamberg, October 2006), University of Bamberg, Germany.Google Scholar
[30] Sinclair, A. J. and Jerrum, M. R. (1989). Approximate counting, uniform generation and rapidly mixing Markov chains. Inf. Comput. 82, 93–133.Google Scholar
[31] Sokal, A. D. (1989). {Monte Carlo methods in statistical mechanics: foundations and new algorithm.} Lecture Notes: Cours de Troisieme Cycle de la Physique en Suisse Romande (Lausanne, June 1989). Unpublished manuscript.Google Scholar