Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T05:16:54.116Z Has data issue: false hasContentIssue false
  • English
  • Français

The extinction time of a general birth and death process with catastrophes

Published online by Cambridge University Press:  24 August 2016

P. J. Brockwell
P. J. Brockwell*
Affiliation:
Colorado State University
*
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

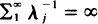The Laplace transform of the extinction time is determined for a general birth and death process with arbitrary catastrophe rate and catastrophe size distribution. It is assumed only that the birth rates satisfy λ0 = 0, λ j > 0 for each j > 0, and . Necessary and sufficient conditions for certain extinction of the population are derived. The results are applied to the linear birth and death process (λ j = jλ, µj = jμ) with catastrophes of several different types.

Keywords

MARKOVIAN POPULATION MODELEXTINCTION TIME
Type
Research Paper
Information
Journal of Applied Probability , Volume 23 , Issue 4 , December 1986 , pp. 851 - 858
Copyright
Copyright © Applied Probability Trust 1986 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant No. DMS 85 01912

References

Brockwell, P. J. (1985) The extinction time of a birth, death and catastrophe process and of a related diffusion model. Adv. Appl. Prob. 17, 42–52.CrossRefGoogle Scholar
Brockwell, P. J., Gani, J. M. and Resnick, S. I. (1982) Birth, immigration and catastrophe processes. Adv. Appl. Prob. 14, 709–731.CrossRefGoogle Scholar
Brockwell, P. J., Gani, J. M. and Resnick, S. I. (1983) Catastrophe processes with continuous state space. Austral J. Statist. 25, 208–226.Google Scholar
Ewens, W. J., Brockwell, P. J., Gani, J. M. and Resnick, S. I. (1986) Minimum viable population size in the presence of catastrophes. In Viable Populations for Conservation, ed. Soulé, M., Cambridge University Press, Cambridge.Google Scholar
Feller, W. (1967) An Introduction to Probability Theory and its Applications, Vol. I, 3rd edn. Wiley, New York.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. Wiley, New York.Google Scholar
Gripenberg, G. (1983) A stationary distribution for the growth of a population subject to random catastrophes. J. Math. Biol. 17, 371–379.Google Scholar
Hanson, F. B. and Tuckwell, H. C. (1978) Persistence times of populations with large random fluctuations. Theoret. Popn Biol. 14, 46–61.CrossRefGoogle ScholarPubMed
Hanson, F. B. and Tuckwell, H. C. (1981) Logistic growth with random density independent disasters. Theoret. Popn Biol. 19, 1–18.Google Scholar
Kaplan, N., Sudbury, A. and Nilsen, T. (1975) A branching process with disasters. J. Appl. Prob. 12, 47–59.Google Scholar
Murthy, D. N. P. (1981) A model for population extinction. Appl. Math. Modelling 5, 227–230.Google Scholar
Pakes, A. G., Trajstman, A. C. and Brockwell, P. J. (1979) A stochastic model for a replicating population subjected to mass emigration due to population pressure. Math. Biosci. 45, 137–157.Google Scholar
Shaffer, M. L. (1983) Determining minimum viable population size for the grizzly bear. Int. Conf. Bear Res. and Management 5, 133–139.Google Scholar
Trajstman, A. C. (1981) A boundary growth population subjected to emigrations due to population pressure. J. Appl. Prob. 18, 571–582.Google Scholar